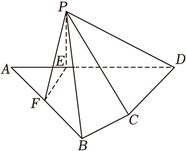
（15分）如图，平面四边形$ABCD$中，$AB=8$，$CD=3$，$AD=5\sqrt{3}$，$\angle ADC=90^\circ$，$\angle BAD=30^\circ$，点$E$，$F$满足$\overrightarrow{AE}=\dfrac{2}{5}\overrightarrow{AD}$，$\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}$，将$\Delta AEF$沿$EF$对折至$\Delta PEF$，使得$PC=4\sqrt{3}$．
（1）证明：$EF\bot PD$；
（2）求面$PCD$与面$PBF$所成的二面角的正弦值．

分析：（1）在$\Delta AEF$中，$AE=\dfrac{2}{5}AD$，$AF=\dfrac{1}{2}AB$，$\angle EAF=30^\circ$，由余弦定理可得$EF$，由勾股定理的逆定理可得$AE\bot EF$，由折叠的性质可知$PE\bot EF$，由线面垂直的判定定理可得$EF\bot$面$PDE$，即可得出答案．
（2）由线面垂直的判定定理可得$PE\bot$面$DEF$，进而可得$EF$，$ED$，$EP$所在直线两两垂直，以$EF$，$ED$，$EP$所在直线分别为$x$，$y$，$z$轴建立空间直角坐标系$E-xyz$，求出平面$PCD$的法向量$\overrightarrow{{n}_{1}}=(x_{1}$，$y_{1}$，$z_{1})$，平面$PBF$的法向量$\overrightarrow{{n}_{2}}=(x_{2}$，$y_{2}$，$z_{2})$，设平面$PCD$与平面$PBF$所成的二面角为$\alpha$，计算$\cos   < \overrightarrow{{n}_{1}}$，$\overrightarrow{{n}_{2}} > =\dfrac{\overrightarrow{{n}_{1}}\cdot \overrightarrow{{n}_{2}}}{\vert \overrightarrow{{n}_{1}}\vert \vert \overrightarrow{{n}_{2}}\vert }$，进而可得答案．
解：（1）证明：在$\Delta AEF$中，$AE=\dfrac{2}{5}AD=2\sqrt{3}$，$AF=\dfrac{1}{2}AB=4$，$\angle EAF=30^\circ$，
所以$\cos  \angle AEF=\dfrac{A{E}^{2}+A{F}^{2}-E{F}^{2}}{2AE\cdot AF}=\dfrac{12+16-E{F}^{2}}{2\cdot 2\sqrt{3}\cdot 4}=\dfrac{\sqrt{3}}{2}$，
所以$EF=2$，
所以$EF^{2}+AE^{2}=AF^{2}$，
所以$AE\bot EF$，
所以$DE\bot EF$，
由折叠的性质可知$PE\bot EF$，
又$PE\bigcap DE=E$，$PE$，$DE\subset$面$PDE$，
所以$EF\bot$面$PDE$，
又$PD\subset$面$PDE$，
所以$EF\bot PD$．
（2）$DE=5\sqrt{3}-2\sqrt{3}=3\sqrt{3}$，$CD=3$，$\angle CDE=90^\circ$，
所以$CE^{2}=36$，$CE=6$，
$PE=AE=2\sqrt{3}$，
所以$PE^{2}+CE^{2}=PC^{2}$，
所以$PE\bot CE$，
又因为$PE\bot EF$，$EF\bigcap CE=E$，$EF$，$CE\subset$面$DEF$，
所以$PE\bot$面$DEF$，
又$DE\subset$面$DEF$，
所以$PE\bot ED$，
所以$EF$，$ED$，$EP$所在直线两两垂直，
以$EF$，$ED$，$EP$所在直线分别为$x$，$y$，$z$轴建立空间直角坐标系$E-xyz:$

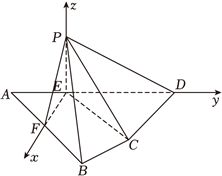
$P(0$，0，$2\sqrt{3})$，$D(0$，$3\sqrt{3}$，$0)$，$F(2$，0，$0)$，$A(0$，$-2\sqrt{3}$，$0)$，则$B(4$，$2\sqrt{3}$，$0)$，$C(3$，$3\sqrt{3}$，$0)$，
所以$\overrightarrow{PD}=(0$，$3\sqrt{3}$，$-2\sqrt{3})$，$\overrightarrow{CD}=(-3$，0，$0)$，$\overrightarrow{PB}=(4$，$2\sqrt{3}$，$-2\sqrt{3})$，$\overrightarrow{BF}=(-2$，$-2\sqrt{3}$，$0)$，
设平面$PCD$的法向量$\overrightarrow{{n}_{1}}=(x_{1}$，$y_{1}$，$z_{1})$，
所以$\begin{cases} \overrightarrow{{n}_{1}}\cdot \overrightarrow{PD}=3\sqrt{3}{y}_{1}-2\sqrt{3}{z}_{1}=0 \\  \overrightarrow{{n}_{1}}\cdot \overrightarrow{CD}=-3{x}_{1}=0\end{cases}$，
设$y_{1}=2$，则$z_{1}=3$，$x_{1}=0$，
所以$\overrightarrow{{n}_{1}}=(0$，2，$3)$，
设平面$PBF$的法向量$\overrightarrow{{n}_{2}}=(x_{2}$，$y_{2}$，$z_{2})$，
所以$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}\cdot \overrightarrow{PB}=4{x}_{2}+2\sqrt{3}{y}_{2}-2\sqrt{3}{z}_{2}=0} \\  {\overrightarrow{{n}_{2}}\cdot \overrightarrow{BF}=-2{x}_{2}-2\sqrt{3}{y}_{2}=0}\end{array}\right.$，
设$x_{2}=\sqrt{3}$，则$y_{2}=-1$，$z_{2}=1$，
所以$\overrightarrow{{n}_{2}}=(\sqrt{3}$，$-1$，$1)$，
设平面$PCD$与平面$PBF$所成的二面角为$\alpha$，
$\cos   < \overrightarrow{{n}_{1}}$，$\overrightarrow{{n}_{2}} > =\dfrac{\overrightarrow{{n}_{1}}\cdot \overrightarrow{{n}_{2}}}{\vert \overrightarrow{{n}_{1}}\vert \vert \overrightarrow{{n}_{2}}\vert }=\dfrac{(0,2,3)\cdot (\sqrt{3},-1,1)}{\sqrt{{2}^{2}+{3}^{2}}\cdot \sqrt{(\sqrt{3})^{2}+(-1)^{2}+{1}^{2}}}=\dfrac{1}{\sqrt{13}\cdot \sqrt{5}}=\dfrac{\sqrt{65}}{65}$，
所以$\sin  \alpha =\dfrac{8\sqrt{65}}{65}$．
点评：本题考查线面的位置关系，二面角，解题中注意转化思想的应用，属于中档题．