（5分）已知正三棱台$ABC-A_{1}B_{1}C_{1}$的体积为$\dfrac{52}{3}$，$AB=6$，$A_{1}B_{1}=2$，则$A_{1}A$与平面$ABC$所成角的正切值为(　　)
A．$\dfrac{1}{2}$              B．1              C．2              D．3
答案：$B$
分析：由正三棱台的体积公式计算出棱台的高$h$，由台体的性质结合线面角的定义求解即可．
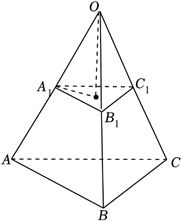
解：设棱台的高为$h$，三条侧棱延长后交于一点$O$，
则由$AB=3A_{1}B_{1}$得：$O$到上底面$A_{1}B_{1}C_{1}$的距离为$\dfrac{1}{2}h$，$O$到下底面$ABC$的距离为$\dfrac{3}{2}h$，

又$S_{\Delta ABC}=\dfrac{\sqrt{3}}{4}\times 6^{2}=9\sqrt{3}$，${S}_{\triangle {A}_{1}{B}_{1}{C}_{1}}=\dfrac{\sqrt{3}}{4}\times 2^{2}=\sqrt{3}$，
所以$V=\dfrac{1}{3}(9\sqrt{3}+\sqrt{3}+\sqrt{9\sqrt{3}\cdot \sqrt{3}})h=\dfrac{52}{3}$，
解得$h=\dfrac{4}{\sqrt{3}}$，
因为上底中心到顶点$A$的距离为$\dfrac{2}{3}\times \dfrac{\sqrt{3}}{2}\times 2=\dfrac{2}{\sqrt{3}}$，
所以$A_{1}A$与平面$ABC$所成角的正切值为$\dfrac{\dfrac{1}{2}h}{\dfrac{2}{\sqrt{3}}}=\dfrac{\sqrt{3}}{4}h=1$．
故选：$B$．
点评：本题主要考查台体的体积公式，空间中直线与平面所成角的求解，属于中档题．