（5分）当$x\in [0，2\pi ]$时，曲线$y=\sin  x$与$y=2\sin  (3x-\dfrac{\pi }{6})$的交点个数为(　　)
A．3              B．4              C．6              D．8
答案：C
分析：作出两函数在$[0$，$2\pi ]$上的图象，结合图象即可得出答案．
解：在同一坐标系中，作出函数$y=\sin  x$与$y=2\sin  (3x-\dfrac{\pi }{6})$在$[0$，$2\pi ]$上的图象如下，

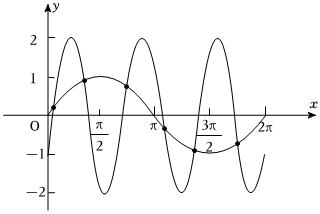
由图象可知，当$x\in [0$，$2\pi ]$时，曲线$y=\sin  x$与$y=2\sin  (3x-\dfrac{\pi }{6})$的交点个数为6个．
故选：C．
点评：本题考查正弦型函数的图象及其运用，考查数形结合思想，属于基础题．