（5分）过原点的一条直线与圆$C:(x+2)^{2}+y^{2}=3$相切，交曲线$y^{2}=2px(p > 0)$于点$P$，若$\vert OP\vert =8$，则$p$的值为 ____．
答案：6．
分析：不妨设直线方程为$y=kx(k > 0)$，由直线与圆相切求解$k$值，可得直线方程，联立直线与抛物线方程，求得$P$点坐标，再由$\vert OP\vert =8$列式求解$p$的值．
解：如图，

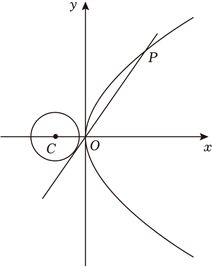
由题意，不妨设直线方程为$y=kx(k > 0)$，即$kx-y=0$，
由圆$C:(x+2)^{2}+y^{2}=3$的圆心$C(-2,0)$到$kx-y=0$的距离为$\sqrt{3}$，
得$\dfrac{\vert -2k\vert }{\sqrt{{k}^{2}+1}}=\sqrt{3}$，解得$k=\sqrt{3}(k > 0)$，
则直线方程为$y=\sqrt{3}x$，
联立$\left\{\begin{array}{l}{y=\sqrt{3}x}\\ {{y}^{2}=2px}\end{array}\right.$，得$\left\{\begin{array}{l}{x=0}\\ {y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=\dfrac{2p}{3}}\\ {y=\dfrac{2\sqrt{3}p}{3}}\end{array}\right.$，即$P(\dfrac{2p}{3},\dfrac{2\sqrt{3}p}{3})$．
可得$\vert OP\vert =\sqrt{(\dfrac{2p}{3})^{2}+(\dfrac{2\sqrt{3}p}{3})^{2}}=8$，解得$p=6$．
故答案为：6．
点评：本题考查直线与圆、直线与抛物线位置关系的应用，考查运算求解能力，是中档题．