（5分）函数$f(x)$的图象如图所示，则$f(x)$的解析式可能为$($　　$)$

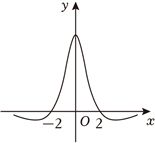
A．$\dfrac{5({{e^x}-{e^{-x}}})}{{x^2}+2}$              B．$\dfrac{5\sin x}{{x^2}+1}$              
C．$\dfrac{5({{e^x}+{e^{-x}}})}{{x^2}+2}$              D．$\dfrac{5\cos x}{{x^2}+1}$
答案：$D$
分析：根据已知条件，结合函数的奇偶性，以及函数的图象，即可求解．
解：由图象可知，$f(x)$图象关于$y$轴对称，为偶函数，故$AB$错误，
当$x > 0$时，$\dfrac{5({e}^{x}+{e}^{-x})}{{x}^{2}+2}$恒大于0，与图象不符合，故$C$错误．
故选：$D$．
点评：本题主要考查函数的图象，属于基础题．