（12分）已知椭圆$C:\dfrac{y^2}{a^2}+\dfrac{x^2}{b^2}=1(a > b > 0)$的离心率为$\dfrac{\sqrt{5}}{3}$，点$A(-2,0)$在$C$上．
（1）求$C$的方程；
（2）过点$(-2,3)$的直线交$C$于点$P$，$Q$两点，直线$AP$，$AQ$与$y$轴的交点分别为$M$，$N$，证明：线段$MN$的中点为定点．
答案：（1）椭圆$C$的方程为$\dfrac{{y}^{2}}{9}+\dfrac{{x}^{2}}{4}=1$；
（2）$MN$的中点为定点$(0,3)$，证明过程见解析．
分析：（1）由题意列关于$a$，$b$，$c$的方程组，求得$a$，$b$，$c$的值，可得椭圆$C$的方程；
（2）设$PQ:y-3=k(x+2)$，即$y=kx+2k+3$，$k < 0$，$P(x_{1}$，$y_{1})$，$Q(x_{2}$，$y_{2})$，联立直线方程与椭圆方程，化为关于$x$的一元二次方程，利用根与系数的关系求得$x_{1}+x_{2}$与$x_{1}x_{2}$的值，写出直线$AP$、$AQ$的方程，求得$M$与$N$的坐标，再由中点坐标公式即可证明$MN$的中点为定点．
解：（1）由题意，$\left\{\begin{array}{l}{\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}}\\ {b=2}\\ {{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=3}\\ {b=2}\\ {c=\sqrt{5}}\end{array}\right.$．
$\therefore$椭圆$C$的方程为$\dfrac{{y}^{2}}{9}+\dfrac{{x}^{2}}{4}=1$；
证明：（2）如图，

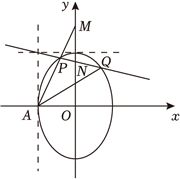
要使过点$(-2,3)$的直线交$C$于点$P$，$Q$两点，则$PQ$的斜率存在且小于0，
设$PQ:y-3=k(x+2)$，即$y=kx+2k+3$，$k < 0$，$P(x_{1}$，$y_{1})$，$Q(x_{2}$，$y_{2})$，
联立$\left\{\begin{array}{l}{y=kx+2k+3}\\ {\dfrac{{y}^{2}}{9}+\dfrac{{x}^{2}}{4}=1}\end{array}\right.$，得$(4k^{2}+9)x^{2}+8k(2k+3)x+16k(k+3)=0$．
△$=[8k(2k+3)]^{2}-4(4k^{2}+9)\cdot 16k(k+3)=-1728k > 0$．
${x}_{1}+{x}_{2}=\dfrac{-8k(2k+3)}{4{k}^{2}+9}$，${x}_{1}{x}_{2}=\dfrac{16k(k+3)}{4{k}^{2}+9}$，
直线$AP:y=\dfrac{{y}_{1}}{{x}_{1}+2}(x+2)$，取$x=0$，得$M(0,\dfrac{2{y}_{1}}{{x}_{1}+2})$；
直线$AQ:y=\dfrac{{y}_{2}}{{x}_{2}+2}(x+2)$，取$x=0$，得$N(0,\dfrac{2{y}_{2}}{{x}_{2}+2})$．
$\therefore$$\dfrac{2{y}_{1}}{{x}_{1}+2}+\dfrac{2{y}_{2}}{{x}_{2}+2}=\dfrac{2{y}_{1}({x}_{2}+2)+2{y}_{2}({x}_{1}+2)}{({x}_{1}+2)({x}_{2}+2)}$
$=2\dfrac{(k{x}_{1}+2k+3)({x}_{2}+2)(k{x}_{2}+2k+3)({x}_{1}+2)}{{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4}$
$=2\dfrac{2k{x}_{1}{x}_{2}+(4k+3)({x}_{1}+{x}_{2})+4(2k+3)}{{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4}$
$=2\dfrac{2k\cdot \dfrac{16k(k+3)}{4{k}^{2}+9}+(4k+3)\cdot \dfrac{-8k(2k+3)}{4{k}^{2}+9}+4(2k+3)}{\dfrac{16k(k+3)}{4{k}^{2}+9}+2\cdot \dfrac{-8k(2k+3)}{4{k}^{2}+9}+4}$
$=2\dfrac{32{k}^{3}+96{k}^{2}-64{k}^{3}-96{k}^{2}-48{k}^{2}-72k+32{k}^{3}+72k+48{k}^{2}+108}{16{k}^{2}+48k-32{k}^{2}-48k+16{k}^{2}+36}$
$=2\times \dfrac{108}{36}=6$．
$\therefore MN$的中点为$(0,3)$，为定点．
点评：本题考查椭圆方程的求法，考查直线与椭圆位置关系的应用，考查运算求解能力，是中档题．