（12分）如图，在三棱锥$P-ABC$中，$AB\bot BC$，$AB=2$，$BC=2\sqrt{2}$，$PB=PC=\sqrt{6}$，$BP$，$AP$，$BC$的中点分别为$D$，$E$，$O$，点$F$在$AC$上，$BF\bot AO$．
（1）求证：$EF//$平面$ADO$；
（2）若$\angle POF=120^\circ$，求三棱锥$P-ABC$的体积．

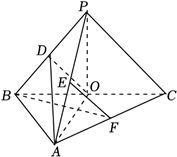
答案：（1）证明见解析；
（2）$\dfrac{2\sqrt{6}}{3}$．
分析：（1）作$FH\bot AB$，垂足为$H$，设$AH=x$，利用$\rm{Rt}\Delta AHF\backsim \rm{Rt}\Delta ABC$得出$HF$，利用$\rm{Rt}\Delta BHF\backsim \rm{Rt}\Delta OBA$列方程求出$x=1$，判断$H$是$AB$的中点，利用中位线定理得出$EF//PC$，$DO//PC$，证明$EF//DO$，得出$EF//$平面$ADO$；
（2）过$P$作$PM$垂直$FO$的延长线交于点$M$，求出$BO$，$PO$，计算$PM$，再求$\Delta ABC$的面积和三棱锥$P-ABC$的体积．
（1）证明：在$\rm{Rt}\Delta ABC$中，作$FH\bot AB$，垂足为$H$，设$AH=x$，则$HB=2-x$，

因为$FH//CB$，所以$\rm{Rt}\Delta AHF\backsim \rm{Rt}\Delta ABC$，所以$\dfrac{AH}{AB}=\dfrac{HF}{BC}$，即$\dfrac{x}{2}=\dfrac{HF}{2\sqrt{2}}$，解得$HF=\sqrt{2}x$，
又因为$\angle BFH=\angle FBO$，所以$\angle AOB=\angle FBH$，且$\angle BHF=\angle OBA=90^\circ$，
所以$\rm{Rt}\Delta BHF\backsim \rm{Rt}\Delta OBA$，所以$\dfrac{HF}{BH}=\dfrac{AB}{BO}$，即$\dfrac{\sqrt{2}x}{2-x}=\dfrac{2}{\sqrt{2}}$，解得$x=1$，
即$AH=1$，所以$H$是$AB$的中点，$F$是$AC$的中点，
又因为$E$是$PA$的中点，所以$EF//PC$，同理，$DO//PC$，所以$EF//DO$，
又因为$EF\not\subset$平面$ADO$，$DO\subset$平面$ADO$，
所以$EF//$平面$ADO$；
（2）解：过$P$作$PM$垂直$FO$的延长线交于点$M$，

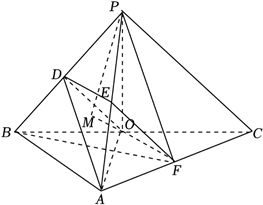
因为$PB=PC$，$O$是$BC$中点，所以$PO\bot BC$，在$\rm{Rt}\Delta PBO$中，$PB=\sqrt{6}$，$BO=\dfrac{1}{2}BC=\sqrt{2}$，所以$PO=\sqrt{PB^2-OB^2}=\sqrt{6-2}=2$，
因为$AB\bot BC$，$OF//AB$，所以$OF\bot BC$，又$PO\bigcap OF=O$，$PO$，$OF\subset$平面$POF$，所以$BC\bot$平面$POF$，
又$PM\subset$平面$POF$，所以$BC\bot PM$，
又$BC\bigcap FM=O$，$BC$，$FM\subset$平面$ABC$，
所以$PM\bot$平面$ABC$，即三棱锥$P-ABC$的高为$PM$，
因为$\angle POF=120^\circ$，所以$\angle POM=60^\circ$，
所以$PM=PO\sin 60^\circ =2\times \dfrac{\sqrt{3}}{2}=\sqrt{3}$，
$\Delta ABC$的面积为$S_{\Delta ABC}=\dfrac{1}{2}\times AB\times BC=\dfrac{1}{2}\times 2\times 2\sqrt{2}=2\sqrt{2}$，
所以三棱锥$P-ABC$的体积为${{V}_{P-ABC}}=\dfrac{1}{3}\times 2\sqrt{2}\times \sqrt{3}=\dfrac{2\sqrt{6}}{3}$．
点评：本题考查了直线与平面平行的应用问题，也考查了几何体体积计算问题，是中档题．