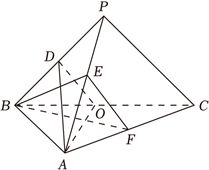
（12分）如图，在三棱锥$P-ABC$中，$AB\bot BC$，$AB=2$，$BC=2\sqrt{2}$，$PB=PC=\sqrt{6}$，$AD=\sqrt{5}DO$，$BP$，$AP$，$BC$的中点分别为$D$，$E$，$O$，点$F$在$AC$上，$BF\bot AO$．
（1）证明：$EF//$平面$ADO$；
（2）证明：平面$ADO\bot$平面$BEF$；
（3）求二面角$D-AO-C$的正弦值．

答案：（1）见解析；（2）见解析；（3）$\dfrac{\sqrt{2}}{2}$．
分析：（1）利用限量法可得$OF//AB$，$OF=\dfrac{1}{2}AB$，四边形$ODEF$为平行四边形，根据线面平行的判定定理即可证明；
（2）由勾股定理可得$AO\bot OD$，$AO\bot EF$，根据面面垂直的判定定理即可证明；
（3）设二面角$D-AO-C$的平面角为$\theta$，可知$\theta$为$\overrightarrow{OD}$和$\overrightarrow{BF}$的夹角，利用向量的夹角公式求解即可．
证明：（1）由题可知，$\vert \overrightarrow{AC}\vert =2\sqrt{3}$，设$\overrightarrow{AF}=\lambda \overrightarrow{AC}$，
$\because$$\overrightarrow{AB}\cdot \overrightarrow{AC}=\vert \overrightarrow{AB}\vert \vert \overrightarrow{AC}\vert \cos \angle BAC=4$，
则$\overrightarrow{BF}\cdot \overrightarrow{AO}=(\lambda \overrightarrow{AC}-\overrightarrow{AB})\cdot (\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC})=\dfrac{\lambda }{2}\vert \overrightarrow{AC}{\vert }^{2}-\dfrac{1}{2}\vert \overrightarrow{AB}{\vert }^{2}+(\dfrac{1}{2}\lambda -\dfrac{1}{2})\overrightarrow{AB}\cdot \overrightarrow{AC}=8\lambda -4=0$，解得$\lambda =\dfrac{1}{2}$，
$\therefore OF//AB$，$OF=\dfrac{1}{2}AB$，
而$DE//AB$，$DE=\dfrac{1}{2}AB$，$\therefore DE//OF$，$DE=OF$，$\therefore$四边形$ODEF$为平行四边形，
$\therefore EF//OD$，
$\because OD\subset$平面$ADO$，$EF\not\subset$平面$ADO$，
$\therefore EF//$平面$ADO$．
证明：（2）$AO=\sqrt{A{B}^{2}+O{B}^{2}}=\sqrt{6}=PC=2OD$，$AD=\sqrt{5}OD$，
$\therefore AD^{2}=AO^{2}+OD^{2}$，即$AO\bot OD$，$AO\bot EF$，
$\because BF\bot AO$，$BF\bigcap EF=F$，
$\therefore AO\bot$平面$BEF$，
$\because AO\subset$平面$ADO$，
$\therefore$平面$ADO\bot$平面$BEF$．
解：（3）设二面角$D-AO-C$的平面角为$\theta$，
$\because AO\bot OD$，$AO\bot BF$，
$\therefore \theta$为$\overrightarrow{OD}$和$\overrightarrow{BF}$的夹角，
$\vert \overrightarrow{BF}\vert =\dfrac{1}{2}\vert \overrightarrow{AC}\vert =\sqrt{3}$，$\vert \overrightarrow{OD}\vert =\dfrac{1}{2}\vert \overrightarrow{PC}\vert =\dfrac{\sqrt{6}}{2}$，
$\cos \theta =\dfrac{\overrightarrow{BF}\cdot \overrightarrow{OD}}{\vert \overrightarrow{BF}\vert \vert \overrightarrow{OD}\vert }=\dfrac{\dfrac{1}{2}(\overrightarrow{OA}-3\overrightarrow{OB})\cdot \overrightarrow{OD}}{\vert \overrightarrow{BF}\vert \vert \overrightarrow{OD}\vert }=\dfrac{-\dfrac{3}{2}\overrightarrow{OB}\cdot \overrightarrow{OD}}{\vert \overrightarrow{BF}\vert \vert \overrightarrow{OD}\vert }=\dfrac{-\dfrac{3}{2}}{\sqrt{3}\times \dfrac{\sqrt{6}}{2}}=-\dfrac{\sqrt{2}}{2}$，
$\sin \theta =\dfrac{\sqrt{2}}{2}$，
$\therefore$二面角$D-AO-C$的正弦值为$\dfrac{\sqrt{2}}{2}$．
点评：本题考查直线与平面、平面与平面位置关系的判定定理，考查二面角的计算，是难题．