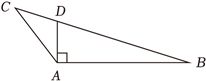
（12分）在$\Delta ABC$中，已知$\angle BAC=120^\circ$，$AB=2$，$AC=1$．
（1）求$\sin \angle ABC$；
（2）若$D$为$BC$上一点．且$\angle BAD=90^\circ$，求$\Delta ADC$的面积．
答案：（1）$\dfrac{\sqrt{21}}{14}$；
（2）$\dfrac{\sqrt{3}}{10}$．
分析：（1）由余弦定理可求$BC$，进而可求$\sin \angle ABC$；
（2）由已知可求$\tan \angle ABC$，进而可得$AD$，可求面积．
解：（1）

在$\Delta ABC$中，由余弦定理可知$BC^{2}=2^{2}+1^{2}-2\times 1\times 2\times \cos 120^\circ =7$，
$BC=\sqrt{7}$，$\therefore$由余弦定理可得$\cos \angle ABC=\dfrac{7+4-1}{2\times \sqrt{7}\times 2}=\dfrac{5\sqrt{7}}{14}$，
又$\angle ABC\in (0^\circ ,60^\circ )$，$\therefore \sin \angle ABC=\sqrt{1-co{s}^{2}\angle ABC}=\sqrt{1-\dfrac{25}{28}}=\dfrac{\sqrt{21}}{14}$，

（2）由（1）知：$\cos \angle ABC=\dfrac{5\sqrt{7}}{14}$，$\sin \angle ABC=\dfrac{\sqrt{21}}{14}$，
$\therefore \tan \angle ABC=\dfrac{\sqrt{3}}{5}$，$\therefore$$\dfrac{1}{2}AD=\dfrac{\sqrt{3}}{5}$，$\therefore AD=\dfrac{2\sqrt{3}}{5}$，
$\therefore \Delta ADC$的面积为$\dfrac{1}{2}\times AD\times AC\times \sin \angle DAC=\dfrac{1}{2}\times \dfrac{2\sqrt{3}}{5}\times 1\times \dfrac{1}{2}=\dfrac{\sqrt{3}}{10}$．
点评：本题考查余弦定理的应用，考查三角形面积的计算，属基础题．