（5分）已知$\Delta ABC$为等腰直角三角形，$AB$为斜边，$\Delta ABD$为等边三角形，若二面角$C-AB-D$为$150^\circ$，则直线$CD$与平面$ABC$所成角的正切值为$($　　$)$
A．$\dfrac{1}{5}$              B．$\dfrac{\sqrt{2}}{5}$              C．$\dfrac{\sqrt{3}}{5}$              D．$\dfrac{2}{5}$
答案：$C$
分析：取$AB$的中点$E$，连接$CE$，$DE$，则根据题意易得二面角$C-AB-D$的平面角为$\angle CED=150^\circ$，又易知平面$CED\bot$平面$ABC$，从而得直线$CD$与平面$ABC$所成角为$\angle DCE$，再解三角形，即可求解．
解：如图，取$AB$的中点$E$，连接$CE$，$DE$，

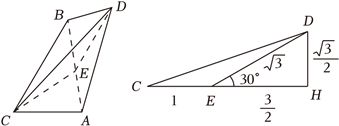
则根据题意易得$AB\bot CE$，$AB\bot DE$，
$\therefore$二面角$C-AB-D$的平面角为$\angle CED=150^\circ$，
$\because AB\bot CE$，$AB\bot DE$，且$CE\bigcap DE=E$，
$\therefore AB\bot$平面$CED$，又$AB\subset$平面$ABC$，
$\therefore$平面$CED\bot$平面$ABC$，
$\therefore CD$在平面$ABC$内的射影为$CE$，
$\therefore$直线$CD$与平面$ABC$所成角为$\angle DCE$，
过$D$作$DH$垂直$CE$所在直线，垂足点为$H$，
设等腰直角三角形$ABC$的斜边长为2，
则可易得$CE=1$，$DE=\sqrt{3}$，又$\angle DEH=30^\circ$，
$\therefore DH=\dfrac{\sqrt{3}}{2}$，$EH=\dfrac{3}{2}$，$\therefore CH=1+\dfrac{3}{2}=\dfrac{5}{2}$，
$\therefore \tan \angle DCE=\dfrac{DH}{CH}=\dfrac{\dfrac{\sqrt{3}}{2}}{\dfrac{5}{2}}=\dfrac{\sqrt{3}}{5}$．
故选：$C$．
点评：本题考查二面角的概念，线面角的求解，化归转化思想，属中档题．