（5分）在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$AB=4$，$O$为$AC_{1}$的中点，若该正方体的棱与球$O$的球面有公共点，则球$O$的半径的取值范围是____．
答案：$[2\sqrt{2}$，$2\sqrt{3}]$．
分析：当球是正方体的外接球时半径最大，当边长为4的正方形是球的大圆的内接正方形时半径达到最小．
解：设球的半径为$R$，
当球是正方体的外接球时，恰好经过正方体的每个顶点，所求的球的半径最大，
若半径变得更大，球会包含正方体，导致球面和棱没有交点，
正方体的外接球直径$2R\prime$为体对角线长$AC_{1}=\sqrt{{4}^{2}+{4}^{2}+{4}^{2}}=4\sqrt{3}$，
即$2R\prime =4\sqrt{3}$，$R\prime =2\sqrt{3}$，故$R_{max}=2\sqrt{3}$，

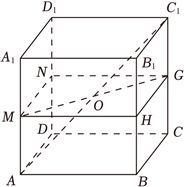
分别取侧枝$AA_{1}$，$BB_{1}$，$CC_{1}$，$DD_{1}$的中点$M$，$H$，$G$，$N$，
则四边形$MNGH$是边长为4的正方形，且$O$为正方形$MNGH$的对角线交点，
连接$MG$，则$MG=4\sqrt{2}$，
当球的一个大圆恰好是四边形$MNGH$的外接圆，球的半径最小，
即$R$的最小值为$2\sqrt{2}$，
综上，球$O$的半径的取值范围是$[2\sqrt{2}$，$2\sqrt{3}]$．
故答案为：$[2\sqrt{2}$，$2\sqrt{3}]$．
点评：本题考查正方体的结构特征、四边形的外接圆、球的结构特征等基础知识，考查运算求解能力，是中档题．