（5分）若$x$，$y$满足约束条件$\left\{{\left.\begin{array}{l}{3x-2y\leqslant 3,}\\ {-2x+3y\leqslant 3}\\ {x+y\geqslant 1,}\end{array}\right.}\right.$，则$z=3x+2y$的最大值为 ____．
答案：15．
分析：作出不等式组对应的平面区域，结合$z$的几何意义，利用数形结合即可得到结论．
解：作出不等式组$\left\{{\left.\begin{array}{l}{3x-2y\leqslant 3,}\\ {-2x+3y\leqslant 3}\\ {x+y\geqslant 1,}\end{array}\right.}\right.$表示的平面区域，如图所示，

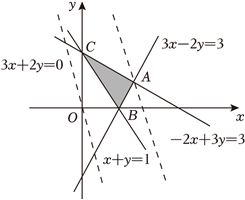
由$z=3x+2y$得$y=-\dfrac{3}{2}x+\dfrac{z}{2}$，
则$\dfrac{z}{2}$表示直线在$y$轴截距，截距越大，$z$越大，
结合图形可知，当直线$y=-\dfrac{3}{2}x+\dfrac{z}{2}$经过点$A$时，$z$最大，
联立$\left\{\begin{array}{l}{3x-2y=3}\\ {-2x+3y=3}\end{array}\right.$可得$A(3,3)$，此时$z$取得最大值15．

点评：本题主要考查线性规划的应用，利用$z$的几何意义，通过数形结合是解决本题的关键，属于中档题．