（5分）函数$y=f(x)$的图象由$y=\cos (2x+\dfrac{\pi }{6})$的图象向左平移$\dfrac{\pi }{6}$个单位长度得到，则$y=f(x)$的图象与直线$y=\dfrac{1}{2}x-\dfrac{1}{2}$的交点个数为$($　　$)$
A．1              B．2              C．3              D．4
答案：$C$
分析：利用三角函数的图象变换，求解函数的解析式，然后判断两个函数的图象交点个数即可．
解：$y=\cos (2x+\dfrac{\pi }{6})$的图象向左平移$\dfrac{\pi }{6}$个单位长度得到$f(x)=\cos (2x+\dfrac{\pi }{2})=-\sin 2x$，
在同一个坐标系中画出两个函数的图象，如图：

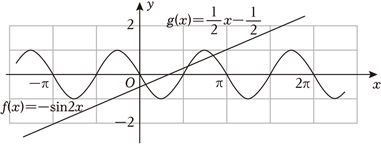
$y=f(x)$的图象与直线$y=\dfrac{1}{2}x-\dfrac{1}{2}$的交点个数为：3．
故选：$C$．
点评：本题考查三角函数的图象的变换，函数的零点个数的求法，考查分析问题解决问题的能力，是中档题．