[选修4-5：不等式选讲]（10分）
23．已知$f(x)=2\vert x-a\vert -a$，$a > 0$．
（1）解不等式$f(x) < x$；
（2）若曲线$y=f(x)$与$x$轴所围成的面积为2，求$a$．
答案：（1）解集为$(\dfrac{a}{3}$，$3a)$，其中$a > 0$；（2）$a=2$．
分析：（1）根据绝对值不等式的解法，化归转化，即可求解；
（2）根据题意可知$f(x)$的对称轴为$x=a$，最低点坐标为$(a,-a)$，再求出$f(x)$的零点，再根据题意建立方程，即可求解．
解：（1）$\because f(x)=2\vert x-a\vert -a$，$a > 0$，
$\therefore f(x) < x$可化为：
$2\vert x-a\vert -a < x$，
$\therefore 2\vert x-a\vert  < x+a$，
$\therefore -(x+a) < 2(x-a) < x+a$，
$\therefore$$\left\{\begin{array}{l}{3x > a}\\ {x < 3a}\end{array}\right.$，又$a > 0$，
$\therefore$$\dfrac{a}{3} < x < 3a$，
$\therefore$原不等式的解集为$(\dfrac{a}{3}$，$3a)$，其中$a > 0$；
（2）$\because f(x)=2\vert x-a\vert -a=\left\{\begin{array}{l}{2x-3a,x\geqslant a}\\ {a-2x,x < a}\end{array}\right.$，$a > 0$，
$\therefore f(x)$的对称轴为$x=a$，且最低点的坐标为$(a,-a)$
令$f(x)=2\vert x-a\vert -a=0$，可得$f(x)$的两零点分别为$x=\dfrac{a}{2}$和$x=\dfrac{3a}{2}$，
函数图象大致如下：

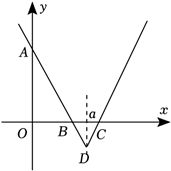
$\therefore$曲线$y=f(x)$与$x$轴所围成的面积为$\dfrac{1}{2}\times (\dfrac{3a}{2}-\dfrac{a}{2})\times a=2$，
$\therefore$解得$a=2$．
点评：本题考查绝对值不等式的解法，函数的性质，化归转化思想，方程思想，属中档题．