（12分）在三棱柱$ABC-A_{1}B_{1}C_{1}$中，$AA_{1}=2$，$A_{1}C\bot$底面$ABC$，$\angle ACB=90^\circ$，$A_{1}$到平面$BCC_{1}B_{1}$的距离为1．
（1）求证：$AC=A_{1}C$；
（2）若直线$AA_{1}$与$BB_{1}$距离为2，求$AB_{1}$与平面$BCC_{1}B_{1}$所成角的正弦值．

答案：（1）证明见解答；
（2）$AB_{1}$与平面$BCC_{1}B_{1}$所成角的正弦值为$\dfrac{\sqrt{13}}{13}$．
分析：（1）取$CC_{1}$的中点，连接$A_{1}O$，可证平面$BCC_{1}B_{1}\bot$平面$A_{1}C_{1}CA$，可得$A_{1}$到$CC_{1}$的距离为1，进而可得$A_{1}O\bot CC_{1}$，可证结论；
（2）过$A$作$AM//A_{1}O$交$C_{1}C$的延长线与$M$，连接$MB_{1}$，取$BB_{1}$的中点$N$，连接$ON$，可证$A_{1}N$为直线$AA_{1}$与$BB_{1}$距离，进而可得$\angle AB_{1}M$为$AB_{1}$与平面$BCC_{1}B_{1}$所成角的角，求解即可．
解：（1）方法一：证明：取$CC_{1}$的中点$O$，连接$A_{1}O$，
$\because A_{1}C\bot$底面$ABC$，$AC\subset$底面$ABC$，
$\therefore A_{1}C\bot AC$，$\therefore A_{1}C\bot A_{1}C_{1}$，$\therefore A_{1}O=\dfrac{1}{2}C_{1}C=1$，
$\because A_{1}$到平面$BCC_{1}B_{1}$的距离为1，点$O\in$平面$BCC_{1}B_{1}$，且$A_{1}O=1$，
$\therefore A_{1}O\bot BCC_{1}B_{1}$，
$\therefore A_{1}O\bot CC_{1}$，
$\because O$为$CC_{1}$的中点，
$\therefore A_{1}C=A_{1}C_{1}=AC$，
$\therefore AC=A_{1}C$；
方法二：证明：取$CC_{1}$的中点$O$，连接$A_{1}O$，
$\because A_{1}C\bot$底面$ABC$，$AC\subset$底面$ABC$，
$\therefore A_{1}C\bot AC$，$\therefore A_{1}C\bot A_{1}C_{1}$，$\therefore A_{1}O=\dfrac{1}{2}C_{1}C=1$，
$\because A_{1}C\bot$底面$ABC$，$BC\subset$底面$ABC$，
$\therefore A_{1}C\bot BC$，$\because \angle ACB=90^\circ$，$\therefore AC\bot BC$，
$\because A_{1}C\bigcap AC=C$，$\therefore BC\bot$平面$A_{1}C_{1}CA$，
$\because BC\subset$平面$BCC_{1}B_{1}$，$\therefore$平面$BCC_{1}B_{1}\bot$平面$A_{1}C_{1}CA$，
$\because A_{1}$到平面$BCC_{1}B_{1}$的距离为1，
$\therefore A_{1}$到$CC_{1}$的距离为1，
$\therefore A_{1}O\bot CC_{1}$，
$\because O$为$CC_{1}$的中点，
$\therefore A_{1}C=A_{1}C_{1}=AC$，
$\therefore AC=A_{1}C$；
（2）过$A$作$AM//A_{1}O$交$C_{1}C$的延长线与$M$，连接$MB_{1}$，
取$BB_{1}$的中点$N$，连接$ON$，

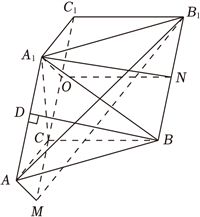
$\therefore$四边形$BCON$为平行四边形，
$\therefore ON\bot$平面$A_{1}C_{1}CA$，
$A_{1}O\bigcap ON=O$，$\therefore CC_{1}\bot$平面$A_{1}ON$，
$\because A_{1}N\subset$平面$A_{1}ON$，
$\therefore CC_{1}\bot A_{1}N$，
$\therefore AA_{1}\bot A_{1}N$，
$\therefore A_{1}N$为直线$AA_{1}$与$BB_{1}$距离，
$\therefore A_{1}N=2$，$\therefore ON=\sqrt{3}$，
由（1）可知$AM\bot$平面$BCC_{1}B_{1}$，
$\therefore \angle AB_{1}M$为$AB_{1}$与平面$BCC_{1}B_{1}$所成角的角，
易求得$C_{1}M=3$，
$\therefore B_{1}M=\sqrt{9+3}=2\sqrt{3}$，
$\because A_{1}M=1$，$\therefore AB_{1}=\sqrt{1+12}=\sqrt{13}$，
$\therefore \sin \angle AB_{1}M=\dfrac{1}{\sqrt{13}}=\dfrac{\sqrt{13}}{13}$．
$\therefore AB_{1}$与平面$BCC_{1}B_{1}$所成角的正弦值为$\dfrac{\sqrt{13}}{13}$．
点评：本题考查线线相等的证明，考查线面角的求法，属中档题．