（5分）设$x$，$y$满足约束条件$\left\{\begin{array}{l}-2x+3y\leqslant 3\\  3x-2y\leqslant 3\\  x+y\geqslant 1\end{array}\right.$，设$z=3x+2y$，则$z$的最大值为 ____．
答案：15．
分析：画出约束条件所表示的平面区域，结合图形确定出目标函数的最优解，代入，即可求解．
解：由题意，作出$x$，$y$满足约束条件$\left\{\begin{array}{l}-2x+3y\leqslant 3\\  3x-2y\leqslant 3\\  x+y\geqslant 1\end{array}\right.$表示的平面区域，如图中阴影部分所示，

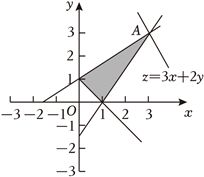
目标函数$z=3x+2y$，可化为直线$y=-\dfrac{3}{2}x+\dfrac{z}{2}$，
由$\left\{\begin{array}{l}{-2x+3y=3}\\ {3x-2y=3}\end{array}\right.$，可得$\left\{\begin{array}{l}{x=3}\\ {y=3}\end{array}\right.$，
即$A(3,3)$，
当直线$y=-\dfrac{3}{2}x+\dfrac{z}{2}$过点$A$时，直线在$y$轴上的截距最大，此时目标函数取得最大值，
代入可得$z_{max}=3\times 3+2\times 3=15$．
故答案为：15．
点评：本题考查了简单的线性规划，属于基础题．