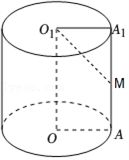
（14分）如图，圆柱下底面与上底面的圆心分别为$O$、$O_{1}$，$AA_{1}$为圆柱的母线，底面半径长为1．
（1）若$AA_{1}=4$，$M$为$AA_{1}$的中点，求直线$MO_{1}$与上底面所成角的大小；（结果用反三角函数值表示）
（2）若圆柱过$OO_{1}$的截面为正方形，求圆柱的体积与侧面积．

分析：（1）转化为解直角三角形问题求解；（2）用圆柱体积和侧面积公式求解．
解：（1）因为$AA_{1}$为圆柱的母线，所以$AA_{1}$垂直于上底面，
所以$\angle MO_{1}A_{1}$是直线$MO_{1}$与上底面所成角，$\tan \angle MO_{1}A_{1}=\dfrac{{A}_{1}M}{{O}_{1}{A}_{1}}=\dfrac{2}{1}=2$，
所以$\angle MO_{1}A_{1}=\arctan 2$．
（2）因为圆柱过$OO_{1}$的截面为正方形，所以$AA_{1}=2$，
所以圆柱的体积为$V=\pi r^{2}h=\pi \cdot 1^{2}\cdot 2=2\pi$，
圆柱的侧面积为$S=2\pi rh=2\pi \cdot 1\cdot 2=4\pi$．

点评：本题考查了直线与平面成角问题，考查了圆柱的体积与侧面积计算问题，属于中档题．