（5分）已知函数$y=f(x)$为定义域为$R$的奇函数，其图像关于$x=1$对称，且当$x\in (0$，$1]$时，$f(x)=\ln x$，若将方程$f(x)=x+1$的正实数根从小到大依次记为$x_{1}$，$x_{2}$，$x_{3}$，$\ldots$，$x_{n}$，则$\mathop{\lim}\limits_{n\rightarrow \infty }(x_{n+1}-x_{n})=$　2　．
分析：$f(x)$是周期为4的周期函数，作出图像，$\mathop{\lim}\limits_{n\rightarrow \infty }(x_{n+1}-x_{n})$的几何意义是两条渐近线之间的距离，由此能求出结果．
解：$\because$函数$y=f(x)$为定义域为$R$的奇函数，其图像关于$x=1$对称，且当$x\in (0$，$1]$时，$f(x)=\ln x$，
$\therefore f(x)$是周期为4的周期函数，图像如图：

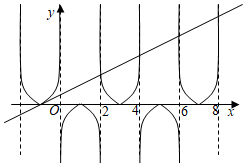
将方程$f(x)=x+1$的正实数根从小到大依次记为$x_{1}$，$x_{2}$，$x_{3}$，$\ldots$，$x_{n}$，
则$\mathop{\lim}\limits_{n\rightarrow \infty }(x_{n+1}-x_{n})$的几何意义是两条渐近线之间的距离2，
$\therefore$$\mathop{\lim}\limits_{n\rightarrow \infty }(x_{n+1}-x_{n})=2$．
故答案为：2．
点评：本题考查极限的求法，考查函数的周期性、函数图像、极限的几何意义等基础知识，考查运算求解能力，是中档题．