（5分）已知$P_{1}(x_{1}$，$y_{1})$，$P_{2}(x_{2}$，$y_{2})$两点均在双曲线$\Gamma :\dfrac{x^2}{a^2}-y^{2}=1(a > 0)$的右支上，若$x_{1}x_{2} > y_{1}y_{2}$恒成立，则实数$a$的取值范围为 　$[1$，$+\infty )$　．
分析：取$P_{2}$的对称点$P_{3}(x_{2}$，$-y_{2})$，结合$x_{1}x_{2} > y_{1}y_{2}$，可得$\overrightarrow{O{P}_{1}}\cdot \overrightarrow{O{P}_{3}} > 0$，然后可得渐近线夹角$\angle MON\leqslant 90^\circ$，代入渐近线斜率计算即可求得．
解：

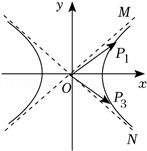
设$P_{2}$的对称点$P_{3}(x_{2}$，$-y_{2})$仍在双曲线右支，由$x_{1}x_{2} > y_{1}y_{2}$，
得$x_{1}x_{2}-y_{1}y_{2} > 0$，即$\overrightarrow{O{P}_{1}}\cdot \overrightarrow{O{P}_{3}} > 0$恒成立，
$\therefore \angle P_{1}OP_{3}$恒为锐角，即$\angle MON\leqslant 90^\circ$，
$\therefore$其中一条渐近线$y=\dfrac{1}{a}x$的斜率$\dfrac{1}{a}\leqslant 1$，
$\therefore a\geqslant 1$，
所以实数$a$的取值范围为$[1$，$+\infty )$．
故答案为：$[1$，$+\infty )$．

点评：本题考查了双曲线的性质，是中档题．