（15分）如图，已知$ABCD$和$CDEF$都是直角梯形，$AB//DC$，$DC//EF$，$AB=5$，$DC=3$，$EF=1$，$\angle BAD=\angle CDE=60^\circ$，二面角$F-DC-B$的平面角为$60^\circ$．设$M$，$N$分别为$AE$，$BC$的中点．
（Ⅰ）证明：$FN\bot AD$；
（Ⅱ）求直线$BM$与平面$ADE$所成角的正弦值．

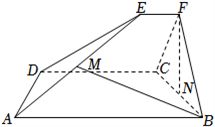
分析：（Ⅰ）根据题意证出$FN\bot$平面$ABCD$，即可得证；（Ⅱ）由于$FN\bot$平面$ABCD$，如图建系，求得平面$ADE$的法向量，代入公式即可求解．
证明：$(I)$由于$CD\bot CB$，$CD\bot CF$，
平面$ABCD\bigcap$平面$CDEF=CD$，$CF\subset$平面$CDEF$，$CB\subset$平面$ABCD$，
所以$\angle FCB$为二面角$F-DC-B$的平面角，
则$\angle FCB=60^\circ$，$CD\bot$平面$CBF$，则$CD\bot FN$．
又$CF=\sqrt{3}(CD-EF)=2\sqrt{3},CB=\sqrt{3}(AB-CD)=2\sqrt{3}$，
则$\Delta BCF$是等边三角形，则$CB\bot FN$，
因为$DC\bot FC$，$DC\bot BC$，$FC\bigcap BC=C$，$FC\subset$平面$FCB$，$BC\subset$平面$FCB$，
所以$DC\bot$平面$FCB$，因为$FN\subset$平面$FCB$，所以$DC\bot FN$，
又因为$DC\bigcap CB=C$，$DC\subset$平面$ABCD$，$CB\subset$平面$ABCD$，
所以$FN\bot$平面$ABCD$，因为$AD\subset$平面$ABCD$，故$FN\bot AD$；
解：（Ⅱ）由于$FN\bot$平面$ABCD$，如图建系：

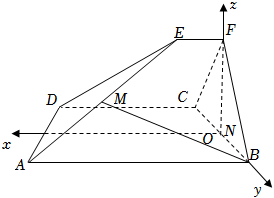
于是$B(0,\sqrt{3},0),A(5,\sqrt{3},0),F(0,0,3),E(1,0,3),D(3,-\sqrt{3},0)$，则$M(3,\dfrac{\sqrt{3}}{2},\dfrac{3}{2})$，
$\overrightarrow{BM}=(3,-\dfrac{\sqrt{3}}{2},\dfrac{3}{2}),\overrightarrow{DA}=(2,2\sqrt{3},0),\overrightarrow{DE}=(-2,\sqrt{3},3)$，
设平面$ADE$的法向量$\overrightarrow{n}=(x$，$y$，$z)$，
则$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{DA}=0}\\ {\overrightarrow{n}\cdot \overrightarrow{DE}=0}\end{array}\right.$，$\therefore$$\left\{\begin{array}{l}{2x+2\sqrt{3}y=0}\\ {-2x+\sqrt{3}y+3z=0}\end{array}\right.$，令$x=\sqrt{3}$，则$y=-1$，$z=\sqrt{3}$，
$\therefore$平面$ADE$的法向量$\overrightarrow{n}=(\sqrt{3},-1,\sqrt{3})$，
设$BM$与平面$ADE$所成角为$\theta$，
则$\sin \theta =\dfrac{\vert \overrightarrow{BM}\cdot n\vert }{\vert \overrightarrow{BM}\vert \vert n\vert }=\dfrac{5\sqrt{7}}{14}$．
点评：本题考查了线线垂直的证明和线面角的计算，属于中档题．