（4分）已知$a$，$b\in R$，若对任意$x\in R$，$a\vert x-b\vert +\vert x-4\vert -\vert 2x-5\vert \geqslant 0$，则(　　)
A．$a\leqslant 1$，$b\geqslant 3$              B．$a\leqslant 1$，$b\leqslant 3$              C．$a\geqslant 1$，$b\geqslant 3$              D．$a\geqslant 1$，$b\leqslant 3$
分析：法一：当$a < 1$，$x\rightarrow +\infty$时，推导出$a\vert x-b\vert +\vert x-4\vert -\vert 2x-5\vert =(a+1-2)x-ab-4+5 < 0$，与已知条件矛盾，从而$a\geqslant 1$，若$b > 3$，则当$x=b$时，推导出$a\vert x-b\vert +\vert x-4\vert -\vert 2x-5\vert =\vert b-4\vert -2b+5 < 0$，与条件矛盾，从而$b\leqslant 3$．
法二：由$a\vert x-b\vert \geqslant \vert 2x-5\vert -\vert x-4\vert$，作出$f(x)=\vert 2x-5\vert -\vert x-4\vert$的图象，数形结合，得$a\geqslant 1$且$b\leqslant 3$．
解法一：当$a < 1$，$x\rightarrow +\infty$时，
$a\vert x-b\vert +\vert x-4\vert -\vert 2x-5\vert =a(x-b)+(x-4)-22+5=(a+1-2)x-ab-4+5 < 0$，与已知条件矛盾，
$\therefore a\geqslant 1$，
若$b > 3$，则当$x=b$时，
$a\vert x-b\vert +\vert x-4\vert -\vert 2x-5\vert =\vert b-4\vert -2b+5 < 0$，与条件矛盾，
$\therefore b\leqslant 3$，
故$ABC$均错误，$D$正确．
解法二：由$a\vert x-b\vert \geqslant \vert 2x-5\vert -\vert x-4\vert$，作出$f(x)=\vert 2x-5\vert -\vert x-4\vert$的图象，如图，

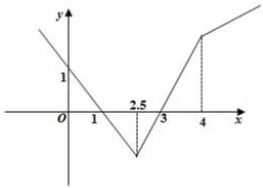
数形结合，得$a\geqslant 1$且$b\leqslant 3$．
故选：$D$．
点评：本题考查绝对值不等式的解法，作为选择题，数形结合法等提高解题效率，属于基础题．