（4分）如图，已知正三棱柱$ABC-A_{1}B_{1}C_{1}$，$AC=AA_{1}$，$E$，$F$分别是棱$BC$，$A_{1}C_{1}$上的点．记$EF$与$AA_{1}$所成的角为$\alpha$，$EF$与平面$ABC$所成的角为$\beta$，二面角$F-BC-A$的平面角为$\gamma$，则(　　)

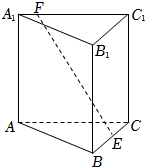
A．$\alpha \leqslant \beta \leqslant \gamma$              B．$\beta \leqslant \alpha \leqslant \gamma$              C．$\beta \leqslant \gamma \leqslant \alpha$              D．$\alpha \leqslant \gamma \leqslant \beta$
分析：根据线线角的定义，线面角的定义，面面角的定义，转化即可求解．
解：$\because$正三棱柱$ABC-A_{1}B_{1}C_{1}$中，$AC=AA_{1}$，
$\therefore$正三棱柱的所有棱长相等，设棱长为1，

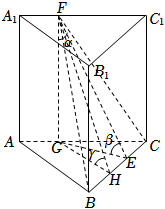
如图，过$F$作$FG\bot AC$，垂足点为$G$，连接$GE$，则$A_{1}A//FG$，
$\therefore EF$与$AA_{1}$所成的角为$\angle EFG=\alpha$，且$\tan \alpha =\dfrac{GE}{FG}=GE$，
又$GE\in [0$，$1]$，$\therefore \tan \alpha \in [0$，$1]$，
$\therefore EF$与平面$ABC$所成的角为$\angle FEG=\beta$，且$\tan \beta =\dfrac{GF}{GE}=\dfrac{1}{GE}\in [1$，$+\infty )$，
$\therefore \tan \beta \geqslant \tan \alpha$，$...$①，
再过$G$点作$GH\bot BC$，垂足点为$H$，连接$HF$，
又易知$FG\bot$底面$ABC$，$BC\subset$底面$ABC$，
$\therefore BC\bot FG$，又$FG\bigcap GH=G$，$\therefore BC\bot$平面$GHF$，
$\therefore$二面角$F-BC-A$的平面角为$\angle GHF=\gamma$，且$\tan \gamma =\dfrac{GF}{GH}=\dfrac{1}{GH}$，又$GH\in [0$，$1]$，
$\therefore \tan \gamma \in [1$，$+\infty )$，$\therefore \tan \gamma \geqslant \tan \alpha$，$...$②，
又$GE\geqslant GH$，$\therefore \tan \beta \leqslant \tan \gamma$，$...$③，
由①②③得$\tan \alpha \leqslant \tan \beta \leqslant \tan \gamma$，又$\alpha$，$\beta$，$\gamma \in [0$，$\dfrac{\pi }{2})$，$y=\tan x$在$[0$，$\dfrac{\pi }{2})$单调递增，
$\therefore \alpha \leqslant \beta \leqslant \gamma$，
故选：$A$．

点评：本题考查线线角的定义，线面角的定义，面面角的定义，考查了转化思想，属中档题．