（4分）某几何体的三视图如图所示（单位：$cm)$，则该几何体的体积（单位：$cm^{3})$是(　　)

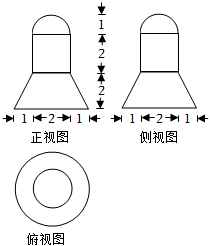
A．$22\pi$              B．$8\pi$              C．$\dfrac{22}{3}\pi$              D．$\dfrac{16}{3}\pi$
分析：判断几何体的形状，利用三视图的数据，求解几何体的体积即可．
解：由三视图可知几何体是上部为半球，中部是圆柱，下部是圆台，
所以几何体的体积为：$\dfrac{1}{2}\times \dfrac{4\pi }{3}\times {1}^{3}+\pi \times 1^{2}\times 2+\dfrac{1}{3}({2}^{2}\times \pi +{1}^{2}\times \pi +\sqrt{{2}^{2}\times \pi \times {1}^{2}\times \pi })\times 2=\dfrac{22}{3}\pi$．
故选：$C$．
点评：本题考查三视图求解几何体的体积，判断几何体的形状是解题的关键，是中档题．