（16分）设有椭圆方程$\Gamma :\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a > b > 0)$，直线$l:x+y-4\sqrt{2}=0$，$\Gamma$下端点为$A$，$M$在$l$上，左、右焦点分别为$F_{1}(-\sqrt{2}$，$0)$、$F_{2}(\sqrt{2}$，$0)$．
（1）$a=2$，$AM$中点在$x$轴上，求点$M$的坐标；
（2）直线$l$与$y$轴交于$B$，直线$AM$经过右焦点$F_{2}$，在$\Delta ABM$中有一内角余弦值为$\dfrac{3}{5}$，求$b$；
（3）在椭圆$\Gamma$上存在一点$P$到$l$距离为$d$，使$\vert PF_{1}\vert +\vert PF_{2}\vert +d=6$，随$a$的变化，求$d$的最小值．

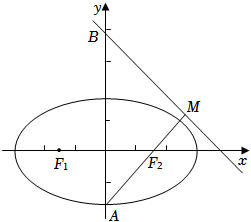
分析：（1）由题意可得椭圆方程为$\dfrac{x^{2}}{4}+\dfrac{y^{2}}{2}=1$，从而确定$M$点的纵坐标，进一步可得点$M$的坐标；
（2）由直线方程可知$B(0,4\sqrt{2})$，分类讨论$\cos \angle BAM=\dfrac{3}{5}$和$\cos \angle BMA=\dfrac{3}{5}$两种情况确定$b$的值即可；
（3）设$P(a\cos \theta ,b\sin \theta )$，利用点到直线距离公式和椭圆的定义可得$\dfrac{\vert a\cos \theta +b\sin \theta -4\sqrt{2}\vert }{\sqrt{2}}=6-2a$，进一步整理计算，结合三角函数的有界性求得$1\leqslant a\leqslant \dfrac{5}{3}$即可确定$d$的最小值．
解：（1）由题意可得$a=2,b=c=\sqrt{2}$，
$\Gamma :\dfrac{x^{2}}{4}+\dfrac{y^{2}}{2}=1,{\;A}(0,-\sqrt{2})$，
$\because AM$的中点在$x$轴上，
$\therefore M$的纵坐标为$\sqrt{2}$，
代入$x+y-4\sqrt{2}=0$得${M}(3\sqrt{2},\sqrt{2})$．
（2）由直线方程可知$B(0,4\sqrt{2})$，
①若$\cos \angle BAM=\dfrac{3}{5}$，则$\tan \angle BAM=\dfrac{4}{3}$，即$\tan \angle OAF_{2}=\dfrac{4}{3}$，
$\therefore$${OA}=\dfrac{3}{4}{OF}_{2}=\dfrac{3}{4}\sqrt{2}$，
$\therefore$${b}=\dfrac{3}{4}\sqrt{2}$．
②若$\cos \angle BMA=\dfrac{3}{5}$，则$\sin \angle BMA=\dfrac{4}{5}$，
$\because$$\angle MBA=\dfrac{\pi }{4}$，$\therefore$$\cos (\angle MBA+\angle AMB)=\dfrac{\sqrt{2}}{2}\times \dfrac{3}{5}-\dfrac{\sqrt{2}}{2}\times \dfrac{4}{5}=-\dfrac{\sqrt{2}}{10}$，
$\therefore$$\cos \angle BAM=\dfrac{\sqrt{2}}{10}$，$\therefore \tan \angle BAM=7$．
即$\tan \angle OAF_{2}=7$，$\therefore$${OA}=\dfrac{\sqrt{2}}{7}$，$\therefore$$b=\dfrac{\sqrt{2}}{7}$，
综上${b}=\dfrac{3}{4}\sqrt{2}$或$\dfrac{\sqrt{2}}{7}$．
（3）设$P(a\cos \theta ,b\sin \theta )$，
由点到直线距离公式可得$\dfrac{\vert a\cos \theta +b\sin \theta -4\sqrt{2}\vert }{\sqrt{2}}=6-2a$，
很明显椭圆在直线的左下方，则$-\dfrac{a\cos \theta +b\sin \theta -4\sqrt{2}}{\sqrt{2}}=6-2a$，
即$4\sqrt{2}-\sqrt{a^{2}+b^{2}}\sin (\theta +\varphi )=6\sqrt{2}-2\sqrt{2}a$，
$\because a^{2}=b^{2}+2$，$\therefore$$\sqrt{2a^{2}-2}\sin (\theta +\varphi )=2\sqrt{2}a-2\sqrt{2}$，
据此可得$\sqrt{a^{2}-1}\sin (\theta +\varphi )=2a-2$，$\vert \sin (\theta +\varphi )\vert =\dfrac{\vert 2a-2\vert }{\sqrt{a^{2}-1}}\leqslant 1$，
整理可得$(a-1)(3a-5)\leqslant 0$，即$1\leqslant a\leqslant \dfrac{5}{3}$，
从而$d=6-2a\geqslant 6-2\times \dfrac{5}{3}=\dfrac{8}{3}$．
即$d$的最小值为$\dfrac{8}{3}$．
点评：本题主要考查椭圆方程的求解，点到直线距离公式及其应用，椭圆中的最值与范围问题等知识，属于中等题．