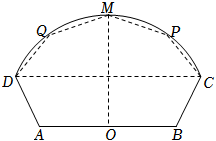
（14分）在如图所示的五边形中，$AD=BC=6$，$AB=20$，$O$为$AB$中点，曲线$CD$上任一点到$O$距离相等，角$\angle DAB=\angle ABC=120^\circ$，$P$，$Q$关于$OM$对称，$MO\bot AB$；
（1）若点$P$与点$C$重合，求$\angle POB$的大小；
（2）$P$在何位置，求五边形面积$S$的最大值．

分析：（1）在$\Delta OBC$中，直接利用余弦定理求出$OP$，再结合正弦定理求解；
（2）利用五边形$CDQMP$的对称性，将所求的面积化为四边形$PMNC$的面积计算问题，充分利用圆弧的性质，找到最大值点，从而解决问题．
解：（1）点$P$与点$C$重合，由题意可得$OB=10$，$BC=6$，$\angle ABC=120^\circ$，
由余弦定理可得$OP^{2}=OB^{2}+BC^{2}-2OB\cdot BC\cos \angle ABC=36+100-2\times 6\times 10\times (-\dfrac{1}{2})=196$，
所以$OP=14$，在$\Delta OBP$中，由正弦定理得$\dfrac{OP}{\sin 120^\circ }=\dfrac{BP}{\sin \angle POB}$，
所以$\dfrac{14}{\dfrac{\sqrt{3}}{2}}=\dfrac{6}{\sin \angle POB}$，解得$\sin \angle POB=\dfrac{3\sqrt{3}}{14}$，
所以$\angle POB$的大小为$\arcsin \dfrac{3\sqrt{3}}{14}$；
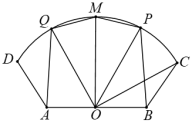
（2）如图，连结$QA$，$PB$，$OQ$，$OP$，
$\because$曲线$CMD$上任意一点到$O$距离相等，
$\therefore OP=OQ=OM=OC=14$，
$\because P$，$Q$关于$OM$对称，
$\therefore P$点在劣弧$CM$中点或劣弧$DM$的中点位置，$S_{\Delta QOM}=S_{\Delta POM}=\alpha$，
则$\angle AOQ=\angle BOP=S_{\Delta BOP}=\dfrac{\pi }{2}-\alpha$，
则五边形面积$S=2(S_{\Delta AOQ}+S_{\Delta QOM})$
$=2[\dfrac{1}{2}\cdot OQ\cdot OA\cdot \sin (\dfrac{\pi }{2}-\alpha )+\dfrac{1}{2}\cdot OQ\cdot OM\cdot \sin \alpha ]$
$=196\sin \alpha +140\cos \alpha$
$=28\sqrt{74}\sin (\alpha +\varphi )$，其中$\tan \varphi =\dfrac{5}{7}$，
当$\sin (\alpha +\varphi )=1$时，${{S}_{MQABP}}$取最大值$28\sqrt{74}$，
$\therefore$五边形$MQABP$面积$S$的最大值为$28\sqrt{74}$．



点评：本题考查了扇形的性质、正、余弦定理和面积公式在解三角形问题中的应用，同时考查了学生的逻辑推理能力、运算能力等，属于中档题．