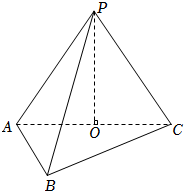
（14分）如图所示三棱锥，底面为等边$\Delta ABC$，$O$为$AC$边中点，且$PO\bot$底面$ABC$，$AP=AC=2$．
（1）求三棱锥体积$V_{P-ABC}$；
（2）若$M$为$BC$中点，求$PM$与面$PAC$所成角大小．

分析：（1）直接利用体积公式求解；
（2）以$O$为坐标原点，$OB$为$x$轴，$OC$为$y$轴，$OP$为$z$轴，建立空间直角坐标系，求得平面$PAC$的法向量，即可求解．
解：（1）在三棱锥$P-ABC$中，因为$PO\bot$底面$ABC$，所以$PO\bot AC$，
又$O$为$AC$边中点，所以$\Delta PAC$为等腰三角形，
又$AP=AC=2$．所以$\Delta PAC$是边长为2的为等边三角形，
$\therefore PO=\sqrt{3}$，三棱锥体积$V_{P-ABC}=\dfrac{1}{3}{S}_{\Delta ABC}\cdot PO=\dfrac{1}{3}\times \dfrac{\sqrt{3}}{4}\times {2}^{2}\times \sqrt{3}=1$，
（2）以$O$为坐标原点，$OB$为$x$轴，$OC$为$y$轴，$OP$为$z$轴，建立空间直角坐标系，

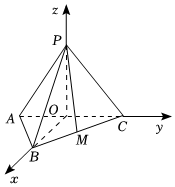
则$P(0$，0，$\sqrt{3})$，$B(\sqrt{3}$，0，$0)$，$C(0$，1，$0)$，$M(\dfrac{\sqrt{3}}{2}$，$\dfrac{1}{2}$，$0)$，
$\overrightarrow{PM}=(\dfrac{\sqrt{3}}{2}$，$\dfrac{1}{2}$，$-\sqrt{3})$，
平面$PAC$的法向量$\overrightarrow{OB}=(\sqrt{3}$，0，$0)$，
设直线$PM$与平面$PAC$所成角为$\theta$，
则直线$PM$与平面$PAC$所成角的正弦值为$\sin \theta =\vert \dfrac{\overrightarrow{PM}\cdot \overrightarrow{OB}}{\vert \overrightarrow{PM}\vert \cdot \vert \overrightarrow{OB}\vert }\vert =\dfrac{\dfrac{3}{2}}{\sqrt{3}\times 2}=\dfrac{\sqrt{3}}{4}$，
所以$PM$与面$PAC$所成角大小为$\arcsin \dfrac{\sqrt{3}}{4}$．
点评：本题考查线面垂直的证明，考查线面角的求法，考查空间中线线、线面间的位置关系等基础知识，考查运算求解能力，是中档题．