（4分）在$\Delta ABC$中，$AC=3$，$BC=4$，$\angle C=90^\circ$．$P$为$\Delta ABC$所在平面内的动点，且$PC=1$，则$\overrightarrow{PA}\cdot \overrightarrow{PB}$的取值范围是(　　)
A．$[-5$，$3]$              B．$[-3$，$5]$              C．$[-6$，$4]$              D．$[-4$，$6]$
分析：根据条件，建立平面直角坐标系，设$P(x,y)$，计算可得$\overrightarrow{PA}\cdot \overrightarrow{PB}=-3x-4y+1$，进而可利用参数方程转化为三角函数的最值问题求解．
解答：解：在$\Delta ABC$中，$AC=3$，$BC=4$，$\angle C=90^\circ$，
以$C$为坐标原点，$CA$，$CB$所在的直线为$x$轴，$y$轴建立平面直角坐标系，如图：

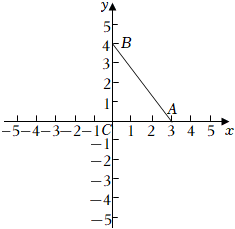
则$A(3,0)$，$B(0,4)$，$C(0,0)$，
设$P(x,y)$，
因为$PC=1$，
所以$x^{2}+y^{2}=1$，
又$\overrightarrow{PA}=(3-x,-y)$，$\overrightarrow{PB}=(-x,4-y)$，
所以$\overrightarrow{PA}\cdot \overrightarrow{PB}=-x(3-x)-y(4-y)=x^{2}+y^{2}-3x-4y=-3x-4y+1$，
设$x=\cos \theta$，$y=\sin \theta$，
所以$\overrightarrow{PA}\cdot \overrightarrow{PB}=-(3\cos \theta +4\sin \theta )+1=-5\sin (\theta +\varphi )+1$，其中$\tan \varphi =\dfrac{3}{4}$，
当$\sin (\theta +\varphi )=1$时，$\overrightarrow{PA}\cdot \overrightarrow{PB}$有最小值为$-4$，
当$\sin (\theta +\varphi )=-1$时，$\overrightarrow{PA}\cdot \overrightarrow{PB}$有最大值为6，
所以$\overrightarrow{PA}\cdot \overrightarrow{PB}\in [-4$，$6]$，
故选：$D$．
点评：本题考查了平面向量数量积的最值问题，属于中档题．