（4分）已知正三棱锥$P-ABC$的六条棱长均为6，$S$是$\Delta ABC$及其内部的点构成的集合．设集合$T=\{Q\in S\vert PQ\leqslant 5\}$，则$T$表示的区域的面积为(　　)
A．$\dfrac{3\pi }{4}$              B．$\pi$              C．$2\pi$              D．$3\pi$
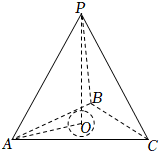
分析：设点$P$在面$ABC$内的投影为点$O$，连接$OA$，根据正三角形的性质求得$OA$的长，并由勾股定理求得$OP$的长，进而知$T$表示的区域是以$O$为圆心，1为半径的圆．
解：设点$P$在面$ABC$内的投影为点$O$，连接$OA$，则$OA=\dfrac{2}{3}\times 3\sqrt{3}=2\sqrt{3}$，
所以$OP=\sqrt{PA^{2}-OA^{2}}=\sqrt{36-12}=2\sqrt{6}$，
由$\sqrt{PQ^{2}-OP^{2}}=\sqrt{25-24}=1$，知$T$表示的区域是以$O$为圆心，1为半径的圆，
所以其面积$S=\pi$．

故选：$B$．
点评：本题考查棱锥的结构特征，点的轨迹问题，考查空间立体感和运算求解能力，属于基础题．