（12分）如图，四面体$ABCD$中，$AD\bot CD$，$AD=CD$，$\angle ADB=\angle BDC$，$E$为$AC$的中点．
（1）证明：平面$BED\bot$平面$ACD$；
（2）设$AB=BD=2$，$\angle ACB=60^\circ$，点$F$在$BD$上，当$\Delta AFC$的面积最小时，求三棱锥$F-ABC$的体积．

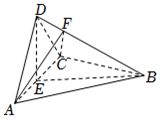
分析：（1）易证$\Delta ADB\cong \Delta CDB$，所以$AC\bot BE$，又$AC\bot DE$，由线面垂直的判定定理可得$AC\bot$平面$BED$，再由面面垂直的判定定理即可证得平面$BED\bot$平面$ACD$；
（2）由题意可知$\Delta ABC$是边长为2的等边三角形，进而求出$BE=\sqrt{3}$，$AC=2$，$AD=CD=\sqrt{2}$，$DE=1$，由勾股定理可得$DE\bot BE$，进而证得$DE\bot$平面$ABC$，连接$EF$，因为$AF=CF$，则$EF\bot AC$，所以当$EF\bot BD$时，$EF$最短，此时$\Delta AFC$的面积最小，求出此时点$F$到平面$ABC$的距离，从而求得此时三棱锥$F-ABC$的体积．
证明：（1）$\because AD=CD$，$\angle ADB=\angle BDC$，$BD=BD$，
$\therefore \Delta ADB\cong \Delta CDB$，
$\therefore AB=BC$，又$\because E$为$AC$的中点．
$\therefore AC\bot BE$，
$\because AD=CD$，$E$为$AC$的中点．
$\therefore AC\bot DE$，又$\because BE\bigcap DE=E$，
$\therefore AC\bot$平面$BED$，
又$\because AC\subset$平面$ACD$，
$\therefore$平面$BED\bot$平面$ACD$；
解：（2）由（1）可知$AB=BC$，
$\therefore AB=BC=2$，$\angle ACB=60^\circ$，$\therefore \Delta ABC$是等边三角形，边长为2，
$\therefore BE=\sqrt{3}$，$AC=2$，$AD=CD=\sqrt{2}$，$DE=1$，
$\because DE^{2}+BE^{2}=BD^{2}$，$\therefore DE\bot BE$，
又$\because DE\bot AC$，$AC\bigcap BE=E$，
$\therefore DE\bot$平面$ABC$，
由（1）知$\Delta ADB\cong \Delta CDB$，$\therefore AF=CF$，连接$EF$，则$EF\bot AC$，
$\therefore S_{\Delta AFC}=\dfrac{1}{2}\times AC\times EF=EF$，
$\therefore$当$EF\bot BD$时，$EF$最短，此时$\Delta AFC$的面积最小，
过点$F$作$FG\bot BE$于点$G$，则$FG//DE$，$\therefore FG\bot$平面$ABC$，
$\because EF=\dfrac{DE\times BE}{BD}=\dfrac{\sqrt{3}}{2}$，
$\therefore BF=\sqrt{B{E}^{2}-E{F}^{2}}=\dfrac{3}{2}$，$\therefore FG=\dfrac{EF\times BF}{BE}=\dfrac{3}{4}$，
$\therefore$三棱锥$F-ABC$的体积$V=\dfrac{1}{3}\times {S}_{\Delta ABC}\times FG=\dfrac{1}{3}\times \dfrac{\sqrt{3}}{4}\times {2}^{2}\times \dfrac{3}{4}=\dfrac{\sqrt{3}}{4}$．

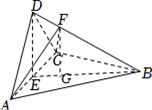
点评：本题主要考查了面面垂直的判定定理，考查了三棱锥的体积公式，同时考查了学生的空间想象能力与计算能力，是中档题．