（12分）如图，四面体$ABCD$中，$AD\bot CD$，$AD=CD$，$\angle ADB=\angle BDC$，$E$为$AC$的中点．
（1）证明：平面$BED\bot$平面$ACD$；
（2）设$AB=BD=2$，$\angle ACB=60^\circ$，点$F$在$BD$上，当$\Delta AFC$的面积最小时，求$CF$与平面$ABD$所成的角的正弦值．

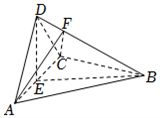
分析：（1）利用三角形全等可得$AB=BC$，可证$EB\bot AC$，易证$DE\bot AC$，从而可证平面$BED\bot$平面$ACD$；
（2）由题意可知$\Delta AFC$的面积最小时，$EF\bot BD$，据此计算可求得$CF$与平面$ABD$所成的角的正弦值．
解答：（1）证明：$\because AD=CD$，$E$为$AC$的中点．$\therefore DE\bot AC$，
又$\because AD=CD$，$\angle ADB=\angle BDC$，$BD=BD$，$\therefore \Delta ABD\cong \Delta CBD$，
$\therefore AB=BC$，又$\because E$为$AC$的中点．$\therefore EB\bot AC$，又$BE\bigcap DE=E$，$BE\subset$平面$BED$，$DE\subset$平面$BED$，
$\therefore AC\bot$平面$BED$，又$AC\subset$平面$ACD$，$\therefore$平面$BED\bot$平面$ACD$；
（2）解：连接$EF$，由（1）知$AC\bot EF$，$\therefore S_{\Delta AFC}=\dfrac{1}{2}AC\times EF$，

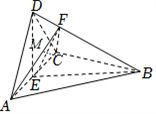
故$EF$最小时，$\Delta AFC$的面积最小，$\therefore EF\bot BD$时，$\Delta AFC$的面积最小，
又$AC\bot$平面$BED$，$BD\subset$平面$BED$，$\therefore AC\bot BD$，又$AC\bigcap EF=E$，$AC\subset$平面$AFC$，$EF\subset$平面$AFC$，
$\therefore BD\bot$平面$AFC$，又$BD\subset$平面$ABD$，$\therefore$平面$ABD\bot$平面$AFC$，
过$C$作$CM\bot AF$于点$M$，则$CM\bot$平面$ABD$，
故$\angle CFM$，即$\angle CFA$为直线$CF$与平面$ABD$所成的角，
由$AB=BD=2$，$\angle ACB=60^\circ$，知$\Delta BAC$是2为边长的等边三角形，
故$AC=2$，由已知可得$DE=1$，$BE=\sqrt{3}$，又$BD=2$，$\therefore BD^{2}=ED^{2}+EB^{2}$，
$\therefore \angle BED=90^\circ$，所以$EF=\dfrac{BE\times DE}{BD}=\dfrac{\sqrt{3}}{2}$，
$\therefore CF=\sqrt{{1}^{2}+\dfrac{3}{4}}=\dfrac{\sqrt{7}}{2}$，$\therefore AF=\dfrac{\sqrt{7}}{2}$，
在$\Delta ACF$中，由余弦定理得$\cos \angle AFC=\dfrac{\dfrac{7}{4}+\dfrac{7}{4}-4}{2\times \dfrac{\sqrt{7}}{2}\times \dfrac{\sqrt{7}}{2}}=-\dfrac{1}{7}$，
$\therefore \sin \angle AFC=\dfrac{4\sqrt{3}}{7}$．
故$CF$与平面$ABD$所成的角的正弦值为$\dfrac{4\sqrt{3}}{7}$．
点评：本题考查面面垂直的证明，考查线面角的正弦值的求法，属中档题．