（5分）函数$f(x)=(3^{x}-3^{-x})\cos x$在区间$[-\dfrac{\pi }{2}$，$\dfrac{\pi }{2}]$的图像大致为(　　)
A．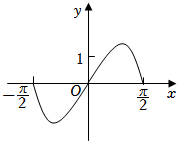              
B．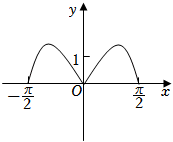              
C．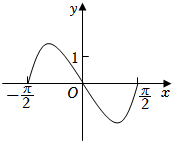              
D．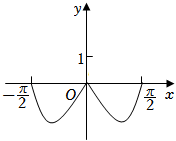
分析：判断函数的奇偶性，结合函数的特殊值判断点的位置，推出选项即可．
解：$f(x)=(3^{x}-3^{-x})\cos x$，
可知$f(-x)=(3^{-x}-3^{x})\cos (-x)=-(3^{x}-3^{-x})\cos x=-f(x)$，
函数是奇函数，排除$BD$；
当$x=1$时，$f$（1）$=(3-3^{-1})\cos 1 > 0$，排除$C$．
故选：$A$．
点评：本题考查函数的奇偶性以及函数的图象的判断，是中档题．