（5分）在长方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，已知$B_{1}D$与平面$ABCD$和平面$AA_{1}B_{1}B$所成的角均为$30^\circ$，则(　　)
A．$AB=2AD$              
B．$AB$与平面$AB_{1}C_{1}D$所成的角为$30^\circ$              
C．$AC=CB_{1}$              
D．$B_{1}D$与平面$BB_{1}C_{1}C$所成的角为$45^\circ$
分析：不妨令$AA_{1}=1$，可根据直线与平面所成角的定义，确定长方体的各棱长，即可求解．
解答：解：如图所示，连接$AB_{1}$，$BD$，不妨令$AA_{1}=1$，

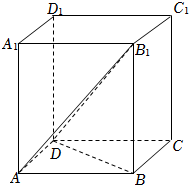
在长方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$AD\bot$面$AA_{1}B_{1}B$，$BB_{1}\bot$面$ABCD$，
所以$\angle B_{1}DB$和$\angle DB_{1}A$分别为$B_{1}D$与平面$ABCD$和平面$AA_{1}B_{1}B$所成的角，
即$\angle B_{1}DB=\angle DB_{1}A=30^\circ$，
所以在$\rm{Rt}\Delta BDB_{1}$中，$BB_{1}=AA_{1}=1$，$BD=\sqrt{3},{B}_{1}D=2$，
在$\rm{Rt}\Delta ADB_{1}$中，$DB_{1}=2$，$AD=1,A{B}_{1}=\sqrt{3}$，
所以$AB=\sqrt{2}$，$C{B}_{1}=\sqrt{2}$，$AC=\sqrt{3}$，
故选项$A$，$C$错误，
由图易知，$AB$在平面$AB_{1}C_{1}D$上的射影在$AB_{1}$上，
所以$\angle B_{1}AB$为$AB$与平面$AB_{1}C_{1}D$所成的角，
在$\rm{Rt}\Delta ABB_{1}$中，$\sin \angle {B}_{1}AB=\dfrac{B{B}_{1}}{A{B}_{1}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}$，
故选项$B$错误，
如图，连接$B_{1}C$，

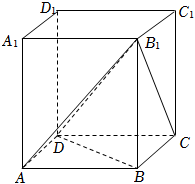
则$B_{1}D$在平面$BB_{1}C_{1}C$上的射影为$B_{1}C$，
所以$\angle DB_{1}C$为$B_{1}D$与平面$BB_{1}C_{1}C$所成的角，
在$Rt$△$DB_{1}C$中，${B}_{1}C=\sqrt{2}=DC$，所以$\angle DB_{1}C=45^\circ$，
所以选项$D$正确，
故选：$D$．
解答：本题考查了直线与平面所成角，属于中档题．