（5分）已知正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$，则(　　)
A．直线$BC_{1}$与$DA_{1}$所成的角为$90^\circ$              
B．直线$BC_{1}$与$CA_{1}$所成的角为$90^\circ$              
C．直线$BC_{1}$与平面$BB_{1}D_{1}D$所成的角为$45^\circ$              
D．直线$BC_{1}$与平面$ABCD$所成的角为$45^\circ$
分析：求出异面直线所成角判断$A$；证明线面垂直，结合线面垂直的性质判断$B$；分别求出线面角判断$C$与$D$．
解：如图，

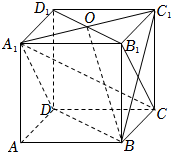
连接$B_{1}C$，由$A_{1}B_{1}//DC$，$A_{1}B_{1}=DC$，得四边形$DA_{1}B_{1}C$为平行四边形，
可得$DA_{1}//B_{1}C$，$\because BC_{1}\bot B_{1}C$，$\therefore$直线$BC_{1}$与$DA_{1}$所成的角为$90^\circ$，故$A$正确；
$\because A_{1}B_{1}\bot BC_{1}$，$BC_{1}\bot B_{1}C$，$A_{1}B_{1}\bigcap B_{1}C=B_{1}$，$\therefore BC_{1}\bot$平面$DA_{1}B_{1}C$，而$CA_{1}\subset$平面$DA_{1}B_{1}C$，
$\therefore BC_{1}\bot CA_{1}$，即直线$BC_{1}$与$CA_{1}$所成的角为$90^\circ$，故$B$正确；
设$A_{1}C_{1}\bigcap B_{1}D_{1}=O$，连接$BO$，可得$C_{1}O\bot$平面$BB_{1}D_{1}D$，即$\angle C_{1}BO$为直线$BC_{1}$与平面$BB_{1}D_{1}D$所成的角，
$\because \sin \angle C_{1}BO=\dfrac{O{C}_{1}}{B{C}_{1}}=\dfrac{1}{2}$，$\therefore$直线$BC_{1}$与平面$BB_{1}D_{1}D$所成的角为$30^\circ$，故$C$错误；
$\because CC_{1}\bot$底面$ABCD$，$\therefore \angle C_{1}BC$为直线$BC_{1}$与平面$ABCD$所成的角为$45^\circ$，故$D$正确．
故选：$ABD$．
点评：本题考查空间中异面直线所成角与线面角的求法，考查空间想象能力与思维能力，考查运算求解能力，是基础题．