16．（5分）在$\Delta ABC$中，$D$为$BC$中点，$E$为$AD$中点，则以下结论：①存在$\Delta ABC$，使得$\overrightarrow{AB}\cdot \overrightarrow{CE}=0$；②存在三角形$\Delta ABC$，使得$\overrightarrow{CE}//(\overrightarrow{CB}+\overrightarrow{CA})$；它们的成立情况是(　　)
A．①成立，②成立              B．①成立，②不成立              
C．①不成立，②成立              D．①不成立，②不成立
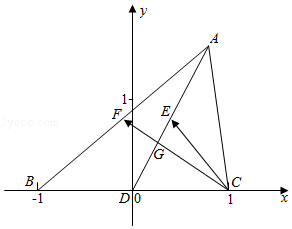
分析：设$A(2x,2y)$，$B(-1,0)$，$C(1,0)$，$D(0,0)$，$E(x,y)$，由向量数量的坐标运算即可判断①；$F$为$AB$中点，可得$(\overrightarrow{CB}+\overrightarrow{CA})=2\overrightarrow{CF}$，由$D$为$BC$中点，可得$CF$与$AD$的交点即为重心$G$，从而可判断②
解：不妨设$A(2x,2y)$，$B(-1,0)$，$C(1,0)$，$D(0,0)$，$E(x,y)$，

①$\overrightarrow{AB}=(-1-2x,-2y)$，$\overrightarrow{CE}=(x-1,y)$，
若$\overrightarrow{AB}\cdot \overrightarrow{CE}=0$，则$-(1+2x)(x-1)-2y^{2}=0$，即$-(1+2x)(x-1)=2y^{2}$，
满足条件的$(x,y)$存在，例如$(0,\dfrac{\sqrt{2}}{2})$，满足上式，所以①成立；
②$F$为$AB$中点，$(\overrightarrow{CB}+\overrightarrow{CA})=2\overrightarrow{CF}$，$CF$与$AD$的交点即为重心$G$，
因为$G$为$AD$的三等分点，$E$为$AD$中点，
所以$\overrightarrow{CE}$与$\overrightarrow{CG}$不共线，即②不成立．
故选：$B$．
点评：本题主要考查平面向量数量积的运算，共线向量的判断，属于中档题．