12．（5分）已知$\theta >0$，存在实数$\varphi$，使得对任意$n\in N^*$，$\cos (n\theta +\varphi )<\dfrac{\sqrt{3}}{2}$，则$\theta$的最小值是____．
分析：在单位圆中分析可得$\theta >\dfrac{\pi }{3}$，由$\dfrac{2\pi }{\theta }\in N^*$，即$\theta =\dfrac{2\pi }{k}$，$k\in N^*$，即可求得$\theta$的最小值．
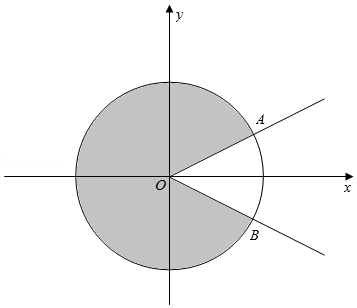
解：在单位圆中分析，由题意可得$n\theta +\varphi$的终边要落在图中阴影部分区域（其中$\angle AOx=\angle BOx=\dfrac{\pi }{6})$，
所以$\theta >\angle AOB=\dfrac{\pi }{3}$，
因为对任意$n\in N^*$都成立，
所以$\dfrac{2\pi }{\theta }\in N^*$，即$\theta =\dfrac{2\pi }{k}$，$k\in N^*$，
同时$\theta >\dfrac{\pi }{3}$，所以$\theta$的最小值为$\dfrac{2\pi }{5}$．
故答案为：$\dfrac{2\pi }{5}$．

点评：本题主要考查三角函数的最值，考查数形结合思想，属于中档题．