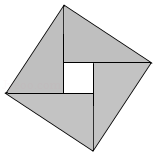
11．（4分）我国古代数学家赵爽用弦图给出了勾股定理的证明．弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形（如图所示）．若直角三角形直角边的长分别为3，4，记大正方形的面积为$S_{1}$，小正方形的面积为$S_{2}$，则$\dfrac{{S}_{1}}{{S}_{2}}=$____．

分析：利用勾股定理求出直角三角形斜边长，即大正方形的边长，由${{S}_{2}}={{S}_{1}}-{{S}_{}}$，求出$S_{2}$，再求出$\dfrac{{S}_{1}}{{S}_{2}}$．
解：$\because$直角三角形直角边的长分别为3，4，
$\therefore$直角三角形斜边的长为$\sqrt{{3}^{2}+{4}^{2}}=5$，
即大正方形的边长为5，$\therefore S_{1}=5^{2}=25$，
则小正方形的面积${{S}_{2}}={{S}_{1}}-{{S}_{}}=25-4\times \dfrac{1}{2}\times 3\times 4=1$，
$\therefore$$\dfrac{{S}_{1}}{{S}_{2}}=25$．
故答案为：25．
点评：本题考查了三角形中的几何计算和勾股定理，考查运算能力，属于基础题．