6．（4分）如图，已知正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$，$M$，$N$分别是$A_{1}D$，$D_{1}B$的中点，则(　　)

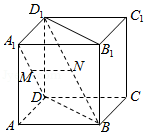
A．直线$A_{1}D$与直线$D_{1}B$垂直，直线$MN//$平面$ABCD$              
B．直线$A_{1}D$与直线$D_{1}B$平行，直线$MN\bot$平面$BDD_{1}B_{1}$              
C．直线$A_{1}D$与直线$D_{1}B$相交，直线$MN//$平面$ABCD$              
D．直线$A_{1}D$与直线$D_{1}B$异面，直线$MN\bot$平面$BDD_{1}B_{1}$
分析：通过证明直线$A_{1}D\bot$平面$ABD_{1}$，$MN$是$\Delta ABD_{1}$的中位线，可判断$A$；根据异面直线的判断可知$A_{1}D$与直线$D_{1}B$是异面直线，可判断$B$；根据异面直线的判断可知直线$A_{1}D$与直线$D_{1}B$是异面直线，可判断$C$；由$MN//AB$，可知$MN$不与平面$BDD_{1}B_{1}$垂直，可判断$D$．
解：连接$AD_{1}$，如图：

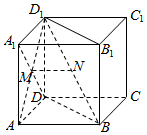
由正方体可知$A_{1}D\bot AD_{1}$，$A_{1}D\bot AB$，$\therefore A_{1}D\bot$平面$ABD_{1}$，
$\therefore A_{1}D\bot D_{1}B$，由题意知$MN$为△$D_{1}AB$的中位线，$\therefore MN//AB$，
又$\because AB\subset$平面$ABCD$，$MN\not\subset$平面$ABCD$，$\therefore MN//$平面$ABCD$．$\therefore A$对；
由正方体可知$A_{1}D$与平面$BDD_{1}$相交于点$D$，$D_{1}B\subset$平面$BDD_{1}$，$D\notin D_{1}B$，
$\therefore$直线$A_{1}D$与直线$D_{1}B$是异面直线，$\therefore B$、$C$错；
$\because MN//AB$，$AB$不与平面$BDD_{1}B_{1}$垂直，$\therefore MN$不与平面$BDD_{1}B_{1}$垂直，$\therefore D$错．
故选：$A$．

点评：本题考查了线面平行的判定定理和线面垂直的判定定理与性质，考查了逻辑推理核心素养，属于中档题．