4．（4分）某几何体的三视图如图所示（单位：$cm)$，则该几何体的体积（单位：$cm^{3})$是(　　)

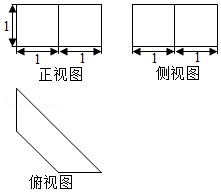
A．$\dfrac{3}{2}$              B．3              C．$\dfrac{3\sqrt{2}}{2}$              D．$3\sqrt{2}$
分析：由三视图还原原几何体，可知该几何体为直四棱柱，底面四边形$ABCD$为等腰梯形，由已知三视图求得对应的量，再由棱柱体积公式求解．
解：由三视图还原原几何体如图，

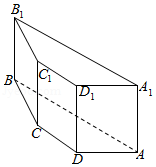
该几何体为直四棱柱，底面四边形$ABCD$为等腰梯形，
其中$AB//CD$，由三视图可知，延长$AD$与$BC$后相交于一点，且$AD\bot BC$，
且$AB=2\sqrt{2}$，$CD=\sqrt{2}$，$AA_{1}=1$，等腰梯形的高为$\sqrt{A{D}^{2}-(\dfrac{AB-CD}{2})^{2}}=\sqrt{1-(\dfrac{\sqrt{2}}{2})^{2}}=\dfrac{\sqrt{2}}{2}$，
则该几何体的体积$V=\dfrac{1}{2}\times (\sqrt{2}+2\sqrt{2})\times \dfrac{\sqrt{2}}{2}\times 1=\dfrac{3}{2}$．
故选：$A$．

点评：本题考查由三视图求面积、体积，关键是由三视图还原原几何体，是中档题．