12．（5分）若斜率为$\sqrt{3}$的直线与$y$轴交于点$A$，与圆$x^{2}+(y-1)^{2}=1$相切于点$B$，则$\vert AB\vert =$____．

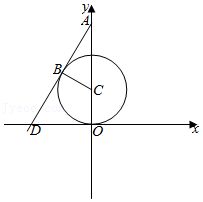
分析：由题意如图可得$AB$与半径$BC$的关系，再由切线的斜率可得$\vert AB\vert$的值．
解假设$A$在$x$轴的上方，斜率为$\sqrt{3}$的直线与$x$轴交于$D$，
则可得$\tan \angle ADO=\sqrt{3}$，所以$\cot \angle BAC=\sqrt{3}$，如图所示，由圆$C$的方程可得，圆的半径为$\vert BC\vert =1$，
由于$B$为切点，所以$AB\bot BC$，所以$\vert AB\vert =\vert BC\vert \cdot \cot \angle BAC=\sqrt{3}$，
故答案为：$\sqrt{3}$．

点评：本题考查直线与圆相切的性质，直线斜率的应用，属于中档题．