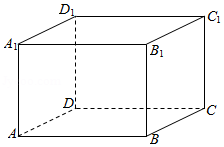
17．（14分）如图，在长方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，已知$AB=BC=2$，$AA_{1}=3$．
（1）若$P$是棱$A_{1}D_{1}$上的动点，求三棱锥$C-PAD$的体积；
（2）求直线$AB_{1}$与平面$ACC_{1}A_{1}$的夹角大小．

分析：（1）直接由三棱锥的体积公式求解即可；
（2）易知直线$AB_{1}$与平面$ACC_{1}A_{1}$所成的角为$\angle OAB_{1}$，求出其正弦值，再由反三角表示即可．
解：（1）如图，在长方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，${{V}_{C-PAD}}=\dfrac{1}{3}{{S}_{\Delta PAD}}\cdot {{h}_{C-PAD}}=\dfrac{1}{3}\times \left( \dfrac{1}{2}\times 2\times 3 \right)\times 2=2$；
（2）

连接$A_{1}C_{1}\bigcap B_{1}D_{1}=O$，
$\because AB=BC$，
$\therefore$四边形$A_{1}B_{1}C_{1}D_{1}$为正方形，则$OB_{1}\bot OA_{1}$，
又$AA_{1}\bot OB_{1}$，$OA_{1}\bigcap AA_{1}=A_{1}$，
$\therefore OB_{1}\bot$平面$ACC_{1}A_{1}$，
$\therefore$直线$AB_{1}$与平面$ACC_{1}A_{1}$所成的角为$\angle OAB_{1}$，
$\therefore$$\sin \angle OA{B}_{1}=\dfrac{O{B}_{1}}{A{B}_{1}}=\dfrac{\dfrac{\sqrt{{2}^{2}+{2}^{2}}}{2}}{\sqrt{{2}^{2}+{3}^{2}}}=\dfrac{\sqrt{26}}{13}$．
$\therefore$直线$AB_{1}$与平面$ACC_{1}A_{1}$所成的角为$\arcsin \dfrac{\sqrt{26}}{13}$．

点评：本题考查三棱锥体积的求法，考查线面角的求解，考查推理能力及运算能力，属于中档题．