11．（5分）已知抛物线$y^{2}=2px(p>0)$，若第一象限的$A$，$B$在抛物线上，焦点为$F$，$\vert AF\vert =2$，$\vert BF\vert =4$，$\vert AB\vert =3$，求直线$AB$的斜率为 ____．
分析：将抛物线上的点到焦点的距离转化为到准线的距离，根据已知条件结合斜率的定义，求出直线$AB$的斜率即可．
解：如图所示，设抛物线的准线为$l$，作$AC\bot l$于点$C$，$BD\bot l$于点$D$，$AE\bot BD$于点$E$，

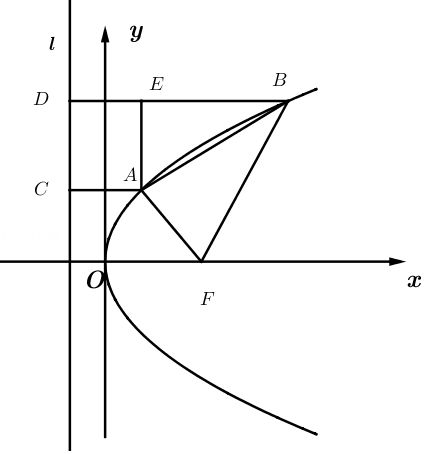
由抛物线的定义，可得$AC=AF=2$，$BD=BF=4$，
$\therefore$$BE=4?2=2,AE=\sqrt{A{B}^{2}?B{E}^{2}}=\sqrt{9?4}=\sqrt{5}$，
$\therefore$直线$AB$的斜率${k}_{AB}=\tan \angle ABE=\dfrac{AE}{BE}=\dfrac{\sqrt{5}}{2}$．
故答案为：$\dfrac{\sqrt{5}}{2}$．
点评：本题主要考查直线斜率的定义与计算，抛物线的定义等知识，属于基础题．