4．（4分）如图正方形$ABCD$的边长为3，求$\overrightarrow{AB}\cdot \overrightarrow{AC}=$____．

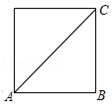
分析：根据$\overrightarrow{AB}\cdot \overrightarrow{AC}=\overrightarrow{AB}\times \overrightarrow{AC}\times \cos \angle BAC$，直接求解即可．
解：由数量积的定义，可得$\overrightarrow{AB}\cdot \overrightarrow{AC}=\overrightarrow{AB}\times \overrightarrow{AC}\times \cos \angle BAC$，
因为$\overrightarrow{AB}=\overrightarrow{AC}\times \cos \angle BAC$，所以$\overrightarrow{AB}\cdot \overrightarrow{AC}={\overrightarrow{AB}}^{2}=9$．
故答案为：9．
点评：本题主要考查平面向量数量积的定义与计算，属于基础题．