19．（15分）已知函数$f(x)=\dfrac{3-2x}{{x}^{2}+a}$．
（1）若$a=0$，求$y=f(x)$在$(1$，$f$（1）$)$处的切线方程；
（2）若函数$f(x)$在$x=-1$处取得极值，求$f(x)$的单调区间，以及最大值和最小值．
分析：（1）求得$a=0$时，$f(x)$的导数，可得切线的斜率和切点，由点斜式方程可得切线的方程；
（2）求得$f(x)$的导数，由题意可得$f\prime (-1)=0$，解得$a$，进而得到$f(x)$和导数，令导数大于0，可得增区间；导数小于0，可得减区间，进而得到所求最值．
解：（1）$f(x)=\dfrac{3-2x}{{x}^{2}}$的导数为$f\prime (x)=\dfrac{-2{x}^{2}-2x(3-2x)}{{x}^{4}}=\dfrac{2x-6}{{x}^{3}}$，
可得$y=f(x)$在$(1,1)$处的切线的斜率为$-4$，
则$y=f(x)$在$(1$，$f$（1）$)$处的切线方程为$y-1=-4(x-1)$，
即为$y=-4x+5$；
（2）$f(x)=\dfrac{3-2x}{{x}^{2}+a}$的导数为$f\prime (x)=\dfrac{-2({x}^{2}+a)-2x(3-2x)}{({x}^{2}+a)^{2}}$，
由题意可得$f\prime (-1)=0$，即$\dfrac{8-2a}{(a+1)^{2}}=0$，解得$a=4$，
可得$f(x)=\dfrac{3-2x}{{x}^{2}+4}$，
$f\prime (x)=\dfrac{2(x+1)(x-4)}{({x}^{2}+4)^{2}}$，
当$x>4$或$x<-1$时，$f\prime (x)>0$，$f(x)$递增；当$-1<x<4$时，$f\prime (x)<0$，$f(x)$递减．
函数$y=f(x)$的图象如右图，当$x\rightarrow -\infty$，$y\rightarrow 0$；$x\rightarrow +\infty$，$y\rightarrow 0$，

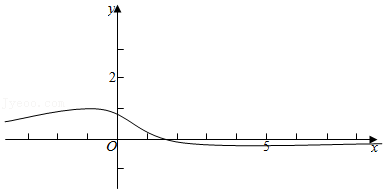
则$f(x)$在$x=-1$处取得极大值1，且为最大值1；在$x=4$处取得极小值$-\dfrac{1}{4}$，且为最小值$-\dfrac{1}{4}$．
所以$f(x)$的增区间为$(-\infty ,-1)$，$(4,+\infty )$，减区间为$(-1,4)$；
$f(x)$的最大值为1，最小值为$-\dfrac{1}{4}$．

点评：本题考查导数的运用：求切线的方程和单调性、极值和最值，考查方程思想和运算能力，属于中档题．