18．（12分）如图，四棱锥$P-ABCD$的底面是矩形，$PD\bot$底面$ABCD$，$M$为$BC$的中点，且$PB\bot AM$．
（1）证明：平面$PAM\bot$平面$PBD$；
（2）若$PD=DC=1$，求四棱锥$P-ABCD$的体积．

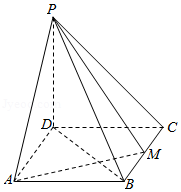
分析：（1）通过线面垂线即可证明；即只需证明$AM\bot$平面$PBD$．
（2）根据$PD\bot$底面$ABCD$，可得$PD$即为四棱锥$P-ABCD$的高，利用体积公式计算即可．
（1）证明：$\because PD\bot$底面$ABCD$，$AM\subset$平面$ABCD$，
$\therefore PD\bot AM$，
又$\because PB\bot AM$，
$PD\bigcap PB=P$，$PB$，$PD\subset$平面$PBD$．
$\therefore AM\bot$平面$PBD$．
$\because AM\subset$平面$PAM$，
$\therefore$平面$PAM\bot$平面$PBD$；
（2）
解：由$PD\bot$底面$ABCD$，
$\therefore PD$即为四棱锥$P-ABCD$的高，$\Delta DPB$是直角三角形；
$\because ABCD$底面是矩形，$PD=DC=1$，$M$为$BC$的中点，且$PB\bot AM$．
设$AD=BC=2a$，取$CP$的中点为$F$．作$EF\bot CD$交于$E$，

连接$MF$，$AF$，$AE$，
可得$MF//PB$，$EF//DP$，
那么$AM\bot MF$．且$EF=\dfrac{1}{2}$．$AE=\sqrt{A{D}^{2}+E{D}^{2}}=\sqrt{\dfrac{1}{4}+4{a}^{2}}$，$AM=\sqrt{A{B}^{2}+B{M}^{2}}=\sqrt{{a}^{2}+1}$，
$AF=\sqrt{E{F}^{2}+A{E}^{2}}$．
$\because \Delta DPB$是直角三角形，
$\therefore$根据勾股定理：$BP=\sqrt{2+4{a}^{2}}$，则$MF=\dfrac{\sqrt{2+4{a}^{2}}}{2}$；
由$\Delta AMF$是直角三角形，
可得$AM^{2}+MF^{2}=AF^{2}$，
解得$a=\dfrac{\sqrt{2}}{2}$．
底面$ABCD$的面积$S=\sqrt{2}$，
则四棱锥$P-ABCD$的体积$V=\dfrac{1}{3}\cdot h\cdot S=\dfrac{1}{3}\times 1\times \sqrt{2}=\dfrac{\sqrt{2}}{3}$．

点评：本题考查平面与平面垂直的判定，考查空间想象能力与思维能力，体积计算，考查运算求解能力，是中档题．