19．（12分）已知直三棱柱$ABC-A_{1}B_{1}C_{1}$中，侧面$AA_{1}B_{1}B$为正方形，$AB=BC=2$，$E$，$F$分别为$AC$和$CC_{1}$的中点，$BF\bot A_{1}B_{1}$．
（1）求三棱锥$F-EBC$的体积；
（2）已知$D$为棱$A_{1}B_{1}$上的点，证明：$BF\bot DE$．

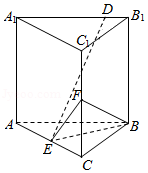
分析：（1）先证明$AB\bot$平面$BCC_{1}B_{1}$，即可得到$AB\bot BC$，再根据直角三角形的性质可知$CE=\sqrt{2}=BE$，最后根据三棱锥的体积公式计算即可；
（2）取$BC$中点$G$，连接$EG$，$B_{1}G$，先证明$EG//AB//B_{1}D$，从而得到$E$、$G$、$B_{1}$、$D$四点共面，再由（1）及线面垂直的性质定理可得$BF\bot EG$，通过角的正切值判断出
$\angle CBF=\angle BB_{1}G$，再通过角的代换可得，$BF\bot B_{1}G$，再根据线面垂直的判定定理可得$BF\bot$平面$EGB_{1}D$，进而得证．
解：（1）在直三棱柱$ABC-A_{1}B_{1}C_{1}$中，$BB_{1}\bot A_{1}B_{1}$，
又$BF\bot A_{1}B_{1}$，$BB_{1}\bigcap BF=B$，$BB_{1}$，$BF\subset$平面$BCC_{1}B_{1}$，
$\therefore A_{1}B_{1}\bot$平面$BCC_{1}B_{1}$，
$\because AB//A_{1}B_{1}$，
$\therefore AB\bot$平面$BCC_{1}B_{1}$，
$\therefore AB\bot BC$，
又$AB=BC$，故$AC=\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$，
$\therefore$$CE=\sqrt{2}=BE$，
而侧面$AA_{1}B_{1}B$为正方形，
$\therefore$$CF=\dfrac{1}{2}C{C}_{1}=\dfrac{1}{2}AB=1$，
$\therefore$$V=\dfrac{1}{3}{S}_{\Delta EBC}\cdot CF=\dfrac{1}{3}\times \dfrac{1}{2}\times \sqrt{2}\times \sqrt{2}\times 1=\dfrac{1}{3}$，即三棱锥$F-EBC$的体积为$\dfrac{1}{3}$；
（2）证明：如图，取$BC$中点$G$，连接$EG$，$B_{1}G$，设$B_{1}G\bigcap BF=H$，

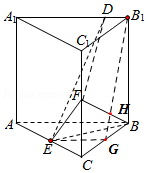
$\because$点$E$是$AC$的中点，点$G$时$BC$的中点，
$\therefore EG//AB$，
$\therefore EG//AB//B_{1}D$，
$\therefore E$、$G$、$B_{1}$、$D$四点共面，
由（1）可得$AB\bot$平面$BCC_{1}B_{1}$，
$\therefore EG\bot$平面$BCC_{1}B_{1}$，
$\therefore BF\bot EG$，
$\because$$\tan \angle CBF=\dfrac{CF}{BC}=\dfrac{1}{2},\tan \angle B{B}_{1}G=\dfrac{BG}{B{B}_{1}}=\dfrac{1}{2}$，且这两个角都是锐角，
$\therefore \angle CBF=\angle BB_{1}G$，
$\therefore \angle BHB_{1}=\angle BGB_{1}+\angle CBF=\angle BGB_{1}+\angle BB_{1}G=90\circ$，
$\therefore BF\bot B_{1}G$，
又$EG\bigcap B_{1}G=G$，$EG$，$B_{1}G\subset$平面$EGB_{1}D$，
$\therefore BF\bot$平面$EGB_{1}D$，
又$DE\subset$平面$EGB_{1}D$，
$\therefore BF\bot DE$．

点评：本题主要考查三棱锥体积的求法以及线线，线面间的垂直关系，考查运算求解能力及逻辑推理能力，属于中档题．