15．（5分）已知函数$f(x)=2\cos (\omega x+\varphi )$的部分图像如图所示，则$f(\dfrac{\pi }{2})=$____．

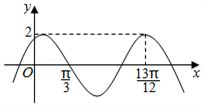
分析：根据图象可得$f(x)$的最小正周期，从而求得$\omega$，然后利用五点作图法可求得$\varphi$，得到$f(x)$的解析式，再计算$f(\dfrac{\pi }{2})$的值．
解：由图可知，$f(x)$的最小正周期$T=\dfrac{4}{3}(\dfrac{13\pi }{12}-\dfrac{\pi }{3})=\pi$，
所以$\omega =\dfrac{2\pi }{T}=2$，因为$f(\dfrac{\pi }{3})=0$，
所以由五点作图法可得$2\times \dfrac{\pi }{3}+\varphi =\dfrac{\pi }{2}$，解得$\varphi =-\dfrac{\pi }{6}$，
所以$f(x)=2\cos (2x-\dfrac{\pi }{6})$，
所以$f(\dfrac{\pi }{2})=2\cos (2\times \dfrac{\pi }{2}-\dfrac{\pi }{6})=-2\cos \dfrac{\pi }{6}=-\sqrt{3}$．
故答案为：$-\sqrt{3}$．
点评：本题主要考查由$y=A\cos (\omega x+\varphi )$的部分图象确定其解析式，考查数形结合思想与运算求解能力，属于基础题．