20．（12分）已知椭圆$C$的方程为$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1(a>b>0)$，右焦点为$F(\sqrt{2}$，$0)$，且离心率为$\dfrac{\sqrt{6}}{3}$．
（Ⅰ）求椭圆$C$的方程；
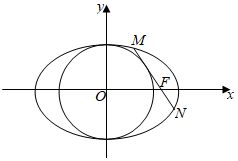
（Ⅱ）设$M$，$N$是椭圆$C$上的两点，直线$MN$与曲线$x^{2}+y^{2}=b^{2}(x>0)$相切．证明：$M$，$N$，$F$三点共线的充要条件是$\vert MN\vert =\sqrt{3}$．
分析：（Ⅰ）利用离心率以及焦点的坐标，求出$a$和$c$的值，结合$a^{2}=b^{2}+c^{2}$，即可求出$b$的值，从而得到椭圆的标准方程；
（Ⅱ）先证明充分性，设直线$MN$的方程，利用圆心到直线的距离公式求出$m$的值，联立直线与椭圆的方程，求出$\vert MN\vert$即可；再证明必要性，设直线$MN$的方程，由圆心到直线的距离公式求出$m$和$t$的关系，联立直线与椭圆的方程，求出$\vert MN\vert$，得到方程，求出$m$和$t$的值，从而得到直线$MN$必过点$F$，即可证明必要性．
（Ⅰ）解：由题意可得，椭圆的离心率$\dfrac{c}{a}=\dfrac{\sqrt{6}}{3}$，又$c=\sqrt{2}$，
所以$a=\sqrt{3}$，则$b^{2}=a^{2}-c^{2}=1$，
故椭圆的标准方程为$\dfrac{{x}^{2}}{3}+{y}^{2}=1$；
（Ⅱ）证明：先证明必要性，
若$M$，$N$，$F$三点共线时，设直线$MN$的方程为$x=my+\sqrt{2}$，
则圆心$O(0,0)$到直线$MN$的距离为$d=\dfrac{\sqrt{2}}{\sqrt{{m}^{2}+1}}=1$，解得$m^{2}=1$，
联立方程组$\left\{\begin{array}{l}{x=my+\sqrt{2}}\\ {\dfrac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$，可得$({m}^{2}+3){y}^{2}+2\sqrt{2}my-1=0$，
即$4{y}^{2}+2\sqrt{2}my-1=0$，
所以$\vert MN\vert =\sqrt{1+{m}^{2}}\cdot \dfrac{\sqrt{8{m}^{2}+16}}{4}=\sqrt{2}\times \dfrac{\sqrt{24}}{4}=\sqrt{3}$；
所以必要性成立；
下面证明充分性，
当$\vert MN\vert =\sqrt{3}$时，设直线$MN$的方程为$x=ty+m$，
此时圆心$O(0,0)$到直线$MN$的距离$d=\dfrac{\vert m\vert }{\sqrt{{t}^{2}+1}}=1$，则$m^{2}-t^{2}=1$，
联立方程组$\left\{\begin{array}{l}{x=ty+m}\\ {\dfrac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$，可得$(t^{2}+3)y^{2}+2tmy+m^{2}-3=0$，
则△$=4t^{2}m^{2}-4(t^{2}+3)(m^{2}-3)=12(t^{2}-m^{2}+3)=24$，
因为$\vert MN\vert =\sqrt{1+{t}^{2}}\cdot \dfrac{\sqrt{24}}{{t}^{2}+3}=\sqrt{3}$，
所以$t^{2}=1$，$m^{2}=2$，
因为直线$MN$与曲线$x^{2}+y^{2}=b^{2}(x>0)$相切，
所以$m>0$，则$m=\sqrt{2}$，
则直线$MN$的方程为$x=ty+\sqrt{2}$恒过焦点$F(\sqrt{2},0)$，
故$M$，$N$，$F$三点共线，
所以充分性得证．
综上所述，$M$，$N$，$F$三点共线的充要条件是$\vert MN\vert =\sqrt{3}$．

点评：本题考查了椭圆标准方程的求解、直线与椭圆位置关系的应用，在解决直线与圆锥曲线位置关系的问题时，一般会联立直线与圆锥曲线的方程，利用韦达定理和“设而不求”的方法进行研究，属于中档题．