|
10.(5分)如图,下列正方体中,$O$为底面的中点,$P$为所在棱的中点,$M$,$N$为正方体的顶点,则满足$MN\bot OP$的是( )
A.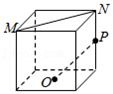 B. B.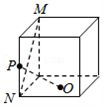
C.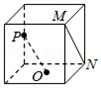 D. D.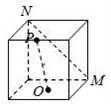
分析:对于$A$,设正方体棱长为2,设$MN$与$OP$所成角为$\theta$,求出$\tan \theta =\dfrac{\sqrt{2}}{2}$,从而不满足$MN\bot OP$;对于$B$,$C$,$D$,作出平面直角坐标系,设正方体棱长为2,利用向量法进行判断.
解:对于$A$,设正方体棱长为2,设$MN$与$OP$所成角为$\theta$,
则$\tan \theta =\dfrac{1}{\dfrac{1}{2}\sqrt{4+4}}=\dfrac{\sqrt{2}}{2}$,$\therefore$不满足$MN\bot OP$,故$A$错误;
对于$B$,如图,作出平面直角坐标系,设正方体棱长为2,

则$N(2$,0,$0)$,$M(0$,0,$2)$,$P(2$,0,$1)$,$O(1$,1,$0)$,
$\overrightarrow{MN}=(2$,0,$-2)$,$\overrightarrow{OP}=(1$,$-1$,$1)$,
$\overrightarrow{MN}\cdot \overrightarrow{OP}=0$,$\therefore$满足$MN\bot OP$,故$B$正确;
对于$C$,如图,作出平面直角坐标系,设正方体棱长为2,

则$M(2$,2,$2)$,$N(0$,2,$0)$,$O(1$,1,$0)$,$P(0$,0,$1)$,
$\overrightarrow{MN}=(-2$,0,$-2)$,$\overrightarrow{OP}=(-1$,$-1$,$1)$,
$\overrightarrow{MN}\cdot \overrightarrow{OP}=0$,$\therefore$满足$MN\bot OP$,故$C$正确;
对于$D$,如图,作出平面直角坐标系,设正方体棱长为2,

则$M(0$,2,$2)$,$N(0$,0,$0)$,$P(2$,1,$2)$,$O(1$,1,$0)$,
$\overrightarrow{MN}=(0$,$-2$,$-2)$,$\overrightarrow{OP}=(1$,0,$2)$,
$\overrightarrow{MN}\cdot \overrightarrow{OP}=-4$,$\therefore$不满足$MN\bot OP$,故$D$错误.
故选:$BC$.
点评:本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系基础知识,考查数学运算、逻辑思维等核心素养,是中档题.
|

