（5分）在正三棱柱$ABC-A_{1}B_{1}C_{1}$中，$AB=AA_{1}=1$，点$P$满足$\overrightarrow{BP}=\lambda \overrightarrow{BC}+\mu \overrightarrow{B{B}_{1}}$，其中$\lambda \in [0$，$1]$，$\mu \in [0$，$1]$，则(　　)
A．当$\lambda =1$时，△$AB_{1}P$的周长为定值              
B．当$\mu =1$时，三棱锥$P-A_{1}BC$的体积为定值              
C．当$\lambda =\dfrac{1}{2}$时，有且仅有一个点$P$，使得$A_{1}P\bot BP$              
D．当$\mu =\dfrac{1}{2}$时，有且仅有一个点$P$，使得$A_{1}B\bot$平面$AB_{1}P$
分析：判断当$\lambda =1$时，点$P$在线段$CC_{1}$上，分别计算点$P$为两个特殊点时的周长，即可判断选项$A$；当$\mu =1$时，点$P$在线段$B_{1}C_{1}$上，利用线面平行的性质以及锥体的体积公式，即可判断选项$B$；当$\lambda =\dfrac{1}{2}$时，取线段$BC$，$B_{1}C_{1}$的中点分别为$M$，$M_{1}$，连结$M_{1}M$，则点$P$在线段$M_{1}M$上，分别取点$P$在$M_{1}$，$M$处，得到均满足$A_{1}P\bot BP$，即可判断选项$C$；当$\mu =\dfrac{1}{2}$时，取$CC_{1}$的中点$D_{1}$，$BB_{1}$的中点$D$，则点$P$在线的$DD_{1}$上，证明当点$P$在点$D_{1}$处时，$A_{1}B\bot$平面$AB_{1}D_{1}$，利用过定点$A$与定直线$A_{1}B$垂直的平面有且只有一个，即可判断选项$D$．
解：对于A，当$\lambda =1$时，$\overrightarrow{BP}=\overrightarrow{BC}+\mu \overrightarrow{B{B}_{1}}$，即$\overrightarrow{CP}=\mu \overrightarrow{B{B}_{1}}$，所以$\overrightarrow{CP}//\overrightarrow{B{B}_{1}}$，
故点$P$在线段$CC_{1}$上，此时△$AB_{1}P$的周长为$AB_{1}+B_{1}P+AP$，
当点$P$为$CC_{1}$的中点时，△$AB_{1}P$的周长为$\sqrt{5}+\sqrt{2}$，
当点$P$在点$C_{1}$处时，△$AB_{1}P$的周长为$2\sqrt{2}+1$，
故周长不为定值，故选项A错误；

对于B，当$\mu =1$时，$\overrightarrow{BP}=\lambda \overrightarrow{BC}+\overrightarrow{B{B}_{1}}$，即$\overrightarrow{{B}_{1}P}=\lambda \overrightarrow{BC}$，所以$\overrightarrow{{B}_{1}P}//\overrightarrow{BC}$，
故点$P$在线段$B_{1}C_{1}$上，
因为$B_{1}C_{1}//$平面$A_{1}BC$，
所以直线$B_{1}C_{1}$上的点到平面$A_{1}BC$的距离相等，
又△$A_{1}BC$的面积为定值，
所以三棱锥$P-A_{1}BC$的体积为定值，故选项B正确；

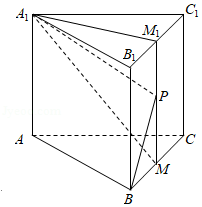
对于C，当$\lambda =\dfrac{1}{2}$时，取线段$BC$，$B_{1}C_{1}$的中点分别为$M$，$M_{1}$，连结$M_{1}M$，
因为$\overrightarrow{BP}=\dfrac{1}{2}\overrightarrow{BC}+\mu \overrightarrow{B{B}_{1}}$，即$\overrightarrow{MP}=\mu \overrightarrow{B{B}_{1}}$，所以$\overrightarrow{MP}//\overrightarrow{B{B}_{1}}$，
则点$P$在线段$M_{1}M$上，
当点$P$在$M_{1}$处时，$A_{1}M_{1}\bot B_{1}C_{1}$，$A_{1}M_{1}\bot B_{1}B$，
又$B_{1}C_{1}\cap B_{1}B=B_{1}$，所以$A_{1}M_{1}\bot$平面$BB_{1}C_{1}C$，
又$BM_{1}\subset$平面$BB_{1}C_{1}C$，所以$A_{1}M_{1}\bot BM_{1}$，即$A_{1}P\bot BP$，
同理，当点$P$在$M$处，$A_{1}P\bot BP$，故选项C错误；

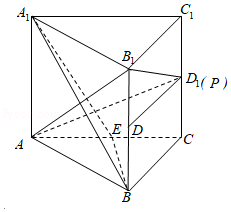
对于D，当$\mu =\dfrac{1}{2}$时，取$CC_{1}$的中点$D_{1}$，$BB_{1}$的中点$D$，
因为$\overrightarrow{BP}=\lambda \overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{B{B}_{1}}$，即$\overrightarrow{DP}=\lambda \overrightarrow{BC}$，所以$\overrightarrow{DP}//\overrightarrow{BC}$，
则点$P$在线的$DD_{1}$上，
当点$P$在点$D_{1}$处时，取$AC$的中点$E$，连结$A_{1}E$，$BE$，
因为$BE\bot$平面$ACC_{1}A_{1}$，又$AD_{1}\subset$平面$ACC_{1}A_{1}$，所以$AD_{1}\bot BE$，
在正方形$ACC_{1}A_{1}$中，$AD_{1}\bot A_{1}E$，
又$BE\cap A_{1}E=E$，$BE$，$A_{1}E\subset$平面$A_{1}BE$，
故$AD_{1}\bot$平面$A_{1}BE$，又$A_{1}B\subset$平面$A_{1}BE$，所以$A_{1}B\bot AD_{1}$，
在正方体形$ABB_{1}A_{1}$中，$A_{1}B\bot AB_{1}$，
又$AD_{1}\cap AB_{1}=A$，$AD_{1}$，$AB_{1}\subset$平面$AB_{1}D_{1}$，所以$A_{1}B\bot$平面$AB_{1}D_{1}$，
因为过定点$A$与定直线$A_{1}B$垂直的平面有且只有一个，
故有且仅有一个点$P$，使得$A_{1}B\bot$平面$AB_{1}P$，故选项D正确．

故选：BD．

点评：本题考查了动点轨迹，线面平行与线面垂直的判定，锥体的体积问题等，综合性强，考查了逻辑推理能力与空间想象能力，属于难题．