（5分）已知点$P$在圆$(x-5)^{2}+(y-5)^{2}=16$上，点$A(4,0)$，$B(0,2)$，则(　　)
A．点$P$到直线$AB$的距离小于10              
B．点$P$到直线$AB$的距离大于2              
C．当$\angle PBA$最小时，$\vert PB\vert =3\sqrt{2}$              
D．当$\angle PBA$最大时，$\vert PB\vert =3\sqrt{2}$
分析：求出过$AB$的直线方程，再求出圆心到直线$AB$的距离，得到圆上的点$P$到直线$AB$的距离范围，判断$A$与$B$；画出图形，由图可知，当过$B$的直线与圆相切时，满足$\angle PBA$最小或最大，求出圆心与$B$点间的距离，再由勾股定理求得$\vert PB\vert$判断$C$与$D$．
解：$\because A(4,0)$，$B(0,2)$，
$\therefore$过$A$、$B$的直线方程为$\dfrac{x}{4}+\dfrac{y}{2}=1$，即$x+2y-4=0$，
圆$(x-5)^{2}+(y-5)^{2}=16$的圆心坐标为$(5,5)$，
圆心到直线$x+2y-4=0$的距离$d=\dfrac{\vert 1\times 5+2\times 5-4\vert }{\sqrt{{1}^{2}+{2}^{2}}}=\dfrac{11}{\sqrt{5}}=\dfrac{11\sqrt{5}}{5}>4$，
$\therefore$点$P$到直线$AB$的距离的范围为$[\dfrac{11\sqrt{5}}{5}-4$，$\dfrac{11\sqrt{5}}{5}+4]$，
$\because$$\dfrac{11\sqrt{5}}{5}<5$，$\therefore$$\dfrac{11\sqrt{5}}{5}-4<1$，$\dfrac{11\sqrt{5}}{5}+4<10$，
$\therefore$点$P$到直线$AB$的距离小于10，但不一定大于2，故$A$正确，$B$错误；
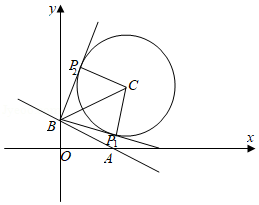
如图，当过$B$的直线与圆相切时，满足$\angle PBA$最小或最大$(P$点位于$P_{1}$时$\angle PBA$最小，位于$P_{2}$时$\angle PBA$最大），
此时$\vert BC\vert =\sqrt{(5-0)^{2}+(5-2)^{2}}=\sqrt{25+9}=\sqrt{34}$，
$\therefore \vert PB\vert =\sqrt{\vert BC{\vert }^{2}-{4}^{2}}=\sqrt{18}=3\sqrt{2}$，故$CD$正确．
故选：ACD．

点评：本题考查直线与圆的位置关系，考查转化思想与数形结合思想，是中档题．